
����Ŀ����ͼ1��ʾ����֪������![]() �Ķ���ΪD����x�ύ��A��B���㣬��y�ύ��C�㣬EΪ�Գ����ϵ�һ�㣬����CE�����߶�CE�Ƶ�E����ʱ�뷽����ת90����C�Ķ�Ӧ��C��ǡ������y���ϣ�
�Ķ���ΪD����x�ύ��A��B���㣬��y�ύ��C�㣬EΪ�Գ����ϵ�һ�㣬����CE�����߶�CE�Ƶ�E����ʱ�뷽����ת90����C�Ķ�Ӧ��C��ǡ������y���ϣ�
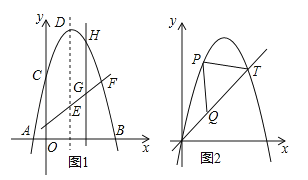
��1��ֱ��д��D���E������ꣻ
��2����FΪֱ��C��E����֪�����ߵ�һ�����㣬��H����������C��F֮���һ�����㣬������H��ֱ��HG��y��ƽ�У�����ֱ��C��E���ڵ�G�����H�ĺ�����Ϊm��0��m��4������ô��mΪ��ֵʱ��![]() =5��6��
=5��6��
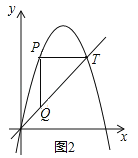
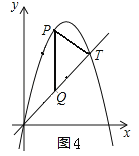
��3��ͼ2��ʾ������������![]() ����ƽ��1����λ��õ��ģ���T��5��y�����������ϣ���P����������O��T֮�������һ�㣬���߶�OT���Ƿ����һ��Q��ʹ��PQT�ǵ���ֱ�������Σ������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�
����ƽ��1����λ��õ��ģ���T��5��y�����������ϣ���P����������O��T֮�������һ�㣬���߶�OT���Ƿ����һ��Q��ʹ��PQT�ǵ���ֱ�������Σ������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��D��2��9����E��2��3������2��![]() ��
��![]() ����3����1��1����3��3����2��2����
����3����1��1����3��3����2��2����
��������
���⣨1�����������䷽�����ɵõ�����ΪD�����꣬Ȼ�����E�������ǣ�2��m������C���������ǣ�0��n����������CEC���ǵ���ֱ�������Σ����E������ꣻ
��2���������ߵ�y=0�������A��B�����꣬Ȼ���ٸ���![]() =5��6���õ���
=5��6���õ���![]() ��Ȼ����֤����HGM�ס�ABN��
��Ȼ����֤����HGM�ס�ABN��![]() ���Ӷ���֤��
���Ӷ���֤��![]() ������HG=5�����H��m����m2+4m+5����G��m��m+1����������HG=5���г�����m�ķ�����⼴�ɣ�
������HG=5�����H��m����m2+4m+5����G��m��m+1����������HG=5���г�����m�ķ�����⼴�ɣ�
��3���ֱ������P����Q����TΪֱ�ǻ���ͼ�Σ�Ȼ�����õ���ֱ�������ε����ʺ�һ�κ�����ͼ���������õ�Q�����꼴�ɣ�
�����������1����������![]() =
=![]() ����D��������ǣ�2��9������EΪ�Գ����ϵ�һ�㣬����E�ĺ�������2�����E�������ǣ�2��m������C���������ǣ�0��n���������߶�CE�Ƶ�E����ʱ�뷽����ת90����C�Ķ�Ӧ��C��ǡ������y���ϣ����CEC���ǵ���ֱ�������Σ���
����D��������ǣ�2��9������EΪ�Գ����ϵ�һ�㣬����E�ĺ�������2�����E�������ǣ�2��m������C���������ǣ�0��n���������߶�CE�Ƶ�E����ʱ�뷽����ת90����C�Ķ�Ӧ��C��ǡ������y���ϣ����CEC���ǵ���ֱ�������Σ���![]() ����ã�
����ã�![]() ��
��![]() ����ȥ��������E�������ǣ�2��3������C���������ǣ�0��1����
����ȥ��������E�������ǣ�2��3������C���������ǣ�0��1����
���ϣ��ɵ�D��������ǣ�2��9������E�������ǣ�2��3����
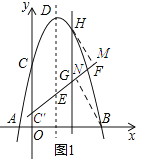
��2����ͼ1��ʾ��
��������![]() ��y=0�ã�
��y=0�ã�![]() ����ã�
����ã�![]() ��
��![]() �����Ե�A����1��0����B��5��0������ֱ��C��E�Ľ���ʽ��
�����Ե�A����1��0����B��5��0������ֱ��C��E�Ľ���ʽ��![]() ����E��2��3����C����0��1���������
����E��2��3����C����0��1���������![]() ����ã�
����ã�![]() ����ֱ��C��E�Ľ���ʽΪ
����ֱ��C��E�Ľ���ʽΪ![]() �������ã�
�������ã�![]() ����ã�
����ã�![]() ����
����![]() ������F������Ϊ��4��5������A����1��0����ֱ��C��E�ϣ���ֱ��C��E�Ľ���ʽΪ
������F������Ϊ��4��5������A����1��0����ֱ��C��E�ϣ���ֱ��C��E�Ľ���ʽΪ![]() �����FAB=45��������B��H�ֱ���BN��AF��HM��AF������ֱ�ΪN��M�����HMN=90������ADN=90�������ߡ�NAD=��HNM=45�������HGM�ס�ABN����
�����FAB=45��������B��H�ֱ���BN��AF��HM��AF������ֱ�ΪN��M�����HMN=90������ADN=90�������ߡ�NAD=��HNM=45�������HGM�ס�ABN����![]() ����
����![]() =5��6����
=5��6����![]() ����
����![]() ����
����![]() ����HG=5�����H�ĺ�����Ϊm�����H��������Ϊ
����HG=5�����H�ĺ�����Ϊm�����H��������Ϊ![]() �����G������Ϊ��m��m+1������
�����G������Ϊ��m��m+1������![]() ����ã�
����ã�![]() ��
��![]() ��
��
��3����ƽ�ƵĹ��ɿ�֪��ƽ�ƺ������ߵĽ���ʽΪ![]() =
=![]() ����x=5����
����x=5����![]() �ã�y=5������T������Ϊ��5��5������ֱ��OT�Ľ���ʽΪ
�ã�y=5������T������Ϊ��5��5������ֱ��OT�Ľ���ʽΪ![]() ����x=5��y=5����ã�k=1����ֱ��OT�Ľ���ʽΪ
����x=5��y=5����ã�k=1����ֱ��OT�Ľ���ʽΪ![]() ��
��
����ͼ2��ʾ����PT��x��ʱ����PTQΪ����ֱ�������Σ�
��y=5����������![]() �ã�
�ã�![]() ����ã�
����ã�![]() ��
��![]() ������P��������1��5������x=1����
������P������Ϊ��1��5������x=1����![]() �ã�y=1������Q������Ϊ��1��1����
�ã�y=1������Q������Ϊ��1��1����
����ͼ3��ʾ��
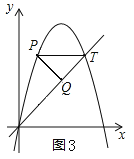
������֪����P������Ϊ��1��5�����ߡ�PTQΪ����ֱ�������Σ�����Q�ĺ�����Ϊ3����x=3����![]() �ã�y=3������Q������Ϊ��3��3����
�ã�y=3������Q������Ϊ��3��3����
����ͼ4��ʾ��
��ֱ��PT����ʽΪ![]() ����ֱ��PT��QT����k=��1����k=��1��x=5��y=5����
����ֱ��PT��QT����k=��1����k=��1��x=5��y=5����![]() �ã�b=10����ֱ��PT�Ľ���ʽΪ
�ã�b=10����ֱ��PT�Ľ���ʽΪ![]() �������ã�
�������ã�![]() ����ã�
����ã�![]() ��
��![]() ������P�ĺ�����Ϊ2����x=2����
������P�ĺ�����Ϊ2����x=2����![]() �ã�y=2������Q������Ϊ��2��2����
�ã�y=2������Q������Ϊ��2��2����
������������Q��������1��1����3��3����2��2����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����m,n����������ʵ�����涨m,n�����ϴ�ĵ�������������������������ֵ������sec(m,n)��ʾ�����磺sec(-1��-2)=-1��sec(1,2)=2,sec(0,0)=0,��������IJ��ϣ�����������⣺
��1��sec(![]() ,3.14)=________,sec(
,3.14)=________,sec(![]() ,
,![]() )=__________;
)=__________;
��2����sec(-3x-1,x+1)=-3x-1,��x��ȡֵ��Χ��
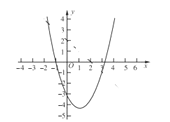
��3������![]() ��
��![]() ��ͼ��Ľ������꣬����
��ͼ��Ľ������꣬����![]() ͼ����ͼ��ʾ��������ͼ����������
ͼ����ͼ��ʾ��������ͼ����������![]() ��ͼ������ͼ��ֱ��д��sec��-x+2,
��ͼ������ͼ��ֱ��д��sec��-x+2, ![]() ������Сֵ��
������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
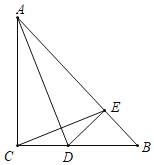
����Ŀ����ͼ���ڡ�ABC�У�AC��BC����C��90�㣬�۵���ABCʹ�õ�C����AB���ϵ�E��������DE��CE�����н��ۣ�����DEB�ǵ���ֱ�������Σ���AB��AC+CD����![]() ����S��CDE��S��BDE��������ȷ�ĸ����ǣ�������
����S��CDE��S��BDE��������ȷ�ĸ����ǣ�������
A. 1B. 2C. 3D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڲ�����װ��������Сһ�����ʵ���ͬ��������һ��Ϊ��ɫ��һ��Ϊ��ɫ��ģ��������һ�����ǰ������Ļ��ᣬ����������������������ʵ�飨������
A. ������һö��ͨ���ӳ���1�㳯�����Ļ���
B. ������һöơ��ƿ�dz��ָ��泯�����Ļ���
C. ������һö�ʵؾ��ȵ�Ӳ�ҳ������泯�����Ļ���
D. ������һö��ͨͼ��������ⴥ�����Ļ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
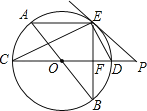
����Ŀ����ͼ��AB��CDΪ��O��ֱ������AE��CD������BE��CD�ڵ�F������E��ֱ��EP��CD���ӳ��߽��ڵ�P��ʹ��PED=��C��
��1����֤��PE�ǡ�O�����ߣ�
��2����֤��EDƽ�֡�BEP��
��3������O�İ뾶Ϊ5��CF=2EF����PD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx��2������A��4��0����B��1��0����
��1����������ߵĽ���ʽ��
��2����D��ֱ��AC�Ϸ����������ϵ�һ�㣬���DCA��������ֵ��
��3��P����������һ���㣬��P��PM��x�ᣬ����ΪM���Ƿ����P�㣬ʹ����A��P��MΪ��������������OAC���ƣ������ڣ���������������ĵ�P�����ꣻ�������ڣ���˵������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
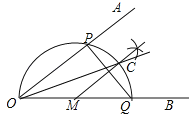
����Ŀ����֪��AOB����ͼ��
����1����OB����ȡһ��M���Ե�MΪԲ�ģ�MO��Ϊ�뾶����Բ���ֱ�OA��OB�ڵ�P��Q��
����2������M��PQ�Ĵ��߽� ![]() �ڵ�C��
�ڵ�C��
����3��������OC��
�������жϣ���![]() =
=![]() ����MC��OA����OP=PQ����OCƽ����AOB��������ȷ�ĸ���Ϊ��������
����MC��OA����OP=PQ����OCƽ����AOB��������ȷ�ĸ���Ϊ��������
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
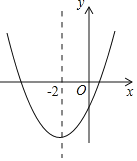
����Ŀ�����κ���y=ax2+bx+c��a��0���Ĵ���ͼ����ͼ��ʾ����������Ϊ����2����9a�������н��ۣ���4a+2b+c��0����5a��b+c=0����������a��x+5����x��1��=��1��������x1��x2����x1��x2����5��x1��x2��1����������|ax2+bx+c|=1���ĸ����������ĸ����ĺ�Ϊ��4��������ȷ�Ľ����У�������
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ABCD�У�AB��6������AC��BD��P�������α��ϻ�Խ�����һ�㣬��PD��2AP����AP�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com