
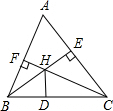
 如图,在△ABC中,∠ABC=60°,∠ACB=54°,BE是AC边上的高,CF是AB边上的高,H是BE和CF的交点,HD是∠BHC的平分线,求∠ABE,∠ACF和∠CHD的度数.
如图,在△ABC中,∠ABC=60°,∠ACB=54°,BE是AC边上的高,CF是AB边上的高,H是BE和CF的交点,HD是∠BHC的平分线,求∠ABE,∠ACF和∠CHD的度数. 分析 由三角形的内角和是180°,可求∠A=66°.又因为BE是AC边上的高,所以∠AEB=90°,所以∠ABE=24°.同理,∠ACF=24度,又因为∠BHC是△CEH的一个外角,所以∠BHC=114°,进而求得∠CHD=57°.
解答 解:∵∠ABC=60°,∠ACB=54°,
∴∠A=180°-∠ABC-∠ACB=180°-60°-54°=66°.
又∵BE是AC边上的高,所以∠AEB=90°,
∴∠ABE=180°-∠BAC-∠AEB=180°-90°-66°=24°.
同理,∠ACF=24°,
∴∠BHC=∠BEC+∠ACF=90°+24°=114°,
∵HD是∠BHC的平分线,
∴∠CHD=$\frac{1}{2}$∠BHC=57°.
点评 此题主要考查了三角形外角的性质及三角形的内角和定理,求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件;三角形的外角通常情况下是转化为内角来解决.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
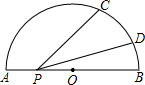 如图,半圆的直径AB=4,P是AB上一动点,C、D在半圆上,$\widehat{BC}$、$\widehat{BD}$的度数分别是75°和15°,则PC+PD的最小值为2$\sqrt{2}$.
如图,半圆的直径AB=4,P是AB上一动点,C、D在半圆上,$\widehat{BC}$、$\widehat{BD}$的度数分别是75°和15°,则PC+PD的最小值为2$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
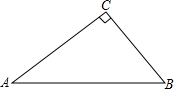 如图,在Rt△ABC中,∠ACB=90°,AB=10,BC=6.若P、Q分别是AB和AC上的动点,则PC+PQ的最小值是$\frac{192}{25}$.
如图,在Rt△ABC中,∠ACB=90°,AB=10,BC=6.若P、Q分别是AB和AC上的动点,则PC+PQ的最小值是$\frac{192}{25}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
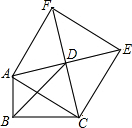 如图,在△ABC中,∠ABC=90°,以AC为一边向三角形外作菱形ACEF,D为菱形ACEF对角线的交点,连接BD,BD平分∠ABC.
如图,在△ABC中,∠ABC=90°,以AC为一边向三角形外作菱形ACEF,D为菱形ACEF对角线的交点,连接BD,BD平分∠ABC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com