
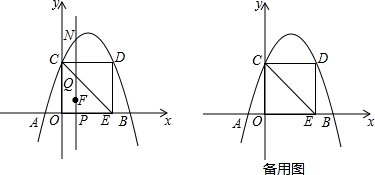
分析 (1)根据待定系数法,可得二次项系数,常数项;
(2)分类讨论:当0<x≤2时,根据正方形的面积公式,可得答案;当2<x≤4时,根据图形割补法,可得答案;当x>4时,根据三角形的面积公式,可得答案;
(3)根据直角三角形的判定:直径所对的圆周角是直角,可得答案.
解答 解:(1)由正方形OCDE的边长为4,得C(0,4),D(4,4),
将C、D点坐标代入函数解析式,得
$\left\{\begin{array}{l}{c=4}\\{16a+\frac{16}{3}+c=4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{1}{3}}\\{c=4}\end{array}\right.$
故答案为:$-\frac{1}{3}$,4;
(2)设yCE=kx+4,把E(4,0)代入
可得4k+4=0∴k=-1
∴yCE=-x+4
∴当x=2时,点F在直线EC上
①当0<x≤2时,如图1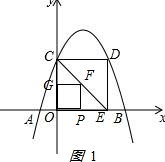 ,S=x2;
,S=x2;
②当2<x≤4时,如图2,OE=4,OP=x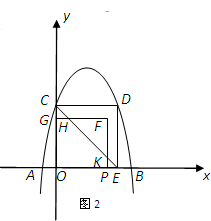
∵Rt△COE和Rt△HFK为等腰直角三角形
∴PE=PK=4-x FK=FH=2x-4
∴S=x2-0.5(2x-4)2=-x2+8x-8;
③当x>4时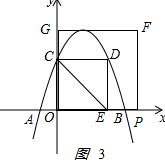 ,
,
S=8;
综上所述:s=$\left\{\begin{array}{l}{{x}^{2}(0<x≤2)}\\{-{x}^{2}+8x-8(2<x≤4)}\\{8(x>4)}\end{array}\right.$
(3)如图4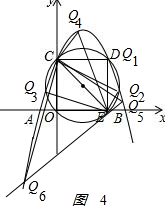 ,
,
利用圆周角定理,得
以CE的长为直径,CE的中点为圆心的圆(x-2)2+(y-2)2=128,
联立直线与抛物线,得
$\left\{\begin{array}{l}{y=-\frac{1}{3}{x}^{2}+\frac{4}{3}x+4}\\{(x-2)^{2}+(y-2)^{2}=128}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=4}\\{y=4}\end{array}\right.$,$\left\{\begin{array}{l}{x=2+\sqrt{7}}\\{y=3}\end{array}\right.$,$\left\{\begin{array}{l}{x=2-\sqrt{7}}\\{y=3}\end{array}\right.$,
即Q1(4,4);Q2(2+$\sqrt{7}$,3);Q3(2-$\sqrt{7}$,3);
∠Q4CE=90°,
联立CQ4、抛物线,得
$\left\{\begin{array}{l}{y=-\frac{1}{3}{x}^{2}+\frac{4}{3}x+4}\\{y=x+4}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=5}\end{array}\right.$
即Q4(1,5);
∠Q5EC=∠Q6EC=90°,Q5E的解析式为y=x-4,
联立Q5E、抛物线,得
$\left\{\begin{array}{l}{y=-\frac{1}{3}{x}^{2}+\frac{4}{3}x+4}\\{y=x-4}\end{array}\right.$,$\left\{\begin{array}{l}{x=\frac{1+\sqrt{97}}{2}}\\{y=\frac{-7+\sqrt{97}}{2}}\end{array}\right.$,$\left\{\begin{array}{l}{x=\frac{1-\sqrt{97}}{2}}\\{y=\frac{-7-\sqrt{97}}{2}}\end{array}\right.$,
即 Q5($\frac{1+\sqrt{97}}{2}$,$\frac{-7+\sqrt{97}}{2}$);Q6($\frac{1-\sqrt{97}}{2}$,$\frac{-7-\sqrt{97}}{2}$);
综上所述:Q1(4,4);Q2(2+$\sqrt{7}$,3);Q3(2-$\sqrt{7}$,3);Q4(1,5);Q5($\frac{1+\sqrt{97}}{2}$,$\frac{-7+\sqrt{97}}{2}$);Q6($\frac{1-\sqrt{97}}{2}$,$\frac{-7-\sqrt{97}}{2}$).
点评 本题考查了二次函数的综合题,(1)利用待定系数法求函数解析式;(2)图形割补法是求面积的关键,分类讨论以防遗漏符合条件的情况;(3)利用圆周角求直角是解题关键.


科目:初中数学 来源: 题型:选择题
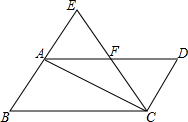 如图,在平行四边形ABCD中,∠B=60°,将△ABC沿对角线AC折叠,点B的对应点落在点E处,且点B,A,E在一条直线上,CE交AD于点F,则图中等边三角形共有( )
如图,在平行四边形ABCD中,∠B=60°,将△ABC沿对角线AC折叠,点B的对应点落在点E处,且点B,A,E在一条直线上,CE交AD于点F,则图中等边三角形共有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
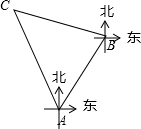 某航班在某日凌晨0:40从甲地(记为A)起飞,沿北偏东35°方向出发,以870km/h的速度直线飞往乙地,但飞机在当日凌晨1:20左右在B处突然改变航向,沿北偏西71°方向飞到C处消失,如果此航班在C处发出求救信号,又测得C在A的北偏西25°方向,求A与求救点C的距离(结果保留整数,参考数据:sin74°≈$\frac{24}{25}$,sin46°≈$\frac{18}{25}$).
某航班在某日凌晨0:40从甲地(记为A)起飞,沿北偏东35°方向出发,以870km/h的速度直线飞往乙地,但飞机在当日凌晨1:20左右在B处突然改变航向,沿北偏西71°方向飞到C处消失,如果此航班在C处发出求救信号,又测得C在A的北偏西25°方向,求A与求救点C的距离(结果保留整数,参考数据:sin74°≈$\frac{24}{25}$,sin46°≈$\frac{18}{25}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com