
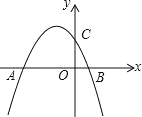
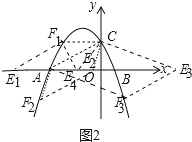
【题目】已知抛物线![]() 与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).
与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).
(1)求抛物线的解析式;
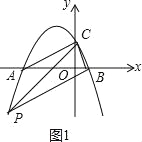
(2)已知点P在抛物线上,连接PC,PB,若△PBC是以BC为直角边的直角三角形,求点P的坐标;
(3)已知点E在x轴上,点F在抛物线上,是否存在以A,C,E,F为顶点的四边形是平行四边形?若存在,请直接写出点E的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)P(-4,0)或(-5,-3);(3)E(-7,0)或(-1,0)或
;(2)P(-4,0)或(-5,-3);(3)E(-7,0)或(-1,0)或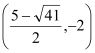 或
或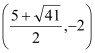 .
.
【解析】
试题分析:(1)把A、B坐标代入解析式可求得抛物线解析式;(2)先证明∠ACB=90°,点A就是所求的点P,求出直线AC解析式,再求出过点B平行AC的直线的解析式,利用方程组即可解决问题.(3)分AC为平行四边形的边,AC为平行四边形的对角线两种切线讨论即可解决问题.
试题解析:(1)把A(-4,0)、B(1,0)坐标代入解析式得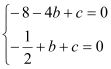 ,解得
,解得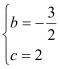 .∴
.∴![]() .(2)当x=0,y═﹣ x2﹣ x+2=2,则C(0,2),∴OC=2,∵A(﹣4,0),B(1,0),
.(2)当x=0,y═﹣ x2﹣ x+2=2,则C(0,2),∴OC=2,∵A(﹣4,0),B(1,0),
∴OA=4,OB=1,AB=5,当∠PCB=90°时,∵AC2=42+22=20,BC2=22+12=5,AB2=52=25,∴AC2+BC2=AB2.∴△ACB是直角三角形,∠ACB=90°,∴当点P与点A重合时,△PBC是以BC为直角边的直角三角形,此时P点坐标为(﹣4,0);当∠PBC=90°时,PB∥AC,如图1,设直线AC的解析式为y=mx+n,则![]() 解得
解得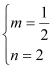 ,∴直线AC的解析式为y= x+2,∵BP∥AC,∴直线BP的解析式为
,∴直线AC的解析式为y= x+2,∵BP∥AC,∴直线BP的解析式为![]() ,把B(1,0)代入得
,把B(1,0)代入得![]() ,解得p=
,解得p=![]() ,∴直线BP的解析式为
,∴直线BP的解析式为![]() ,解方程组
,解方程组 得
得![]() 或
或![]() ,此时P点坐标为(﹣5,﹣3);综上所述,满足条件的P点坐标为(﹣4,0)或(﹣5,﹣3);
,此时P点坐标为(﹣5,﹣3);综上所述,满足条件的P点坐标为(﹣4,0)或(﹣5,﹣3);
(3)存在点E,设点E坐标为(m,0),F![]() .①当AC为边,CF1∥AE1,易知CF1=3,此时E1坐标(﹣7,0),②当AC为边时,AC∥EF,易知点F纵坐标为﹣2,∴
.①当AC为边,CF1∥AE1,易知CF1=3,此时E1坐标(﹣7,0),②当AC为边时,AC∥EF,易知点F纵坐标为﹣2,∴![]() ,解得n=
,解得n=![]() ,得到F2(
,得到F2(![]() ,﹣2),F3(
,﹣2),F3(![]() ,﹣2),∴
,﹣2),∴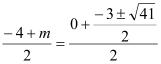 ,解得m=
,解得m=![]() .∴E2
.∴E2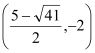 ,E3
,E3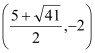 ,③当AC为对角线时,AE4=CF1=3,此时E4(﹣1,0),
,③当AC为对角线时,AE4=CF1=3,此时E4(﹣1,0),
综上所述满足条件的点E坐标为(-7,0)或(-1,0)或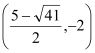 或
或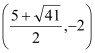 .
.


科目:初中数学 来源: 题型:
【题目】工匠绝技,精益求精,中国船舶重工的钳工顾秋亮凭着精到丝级的手艺,为海底探索者7000米级潜水器“蛟龙号”安装观察窗玻璃,成功地将玻璃与金属窗座之间的缝隙控制在0.2丝米以下已知1丝米=0.0001,0.2丝米=0.00002米,则用科学记数表示数据0.00002为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
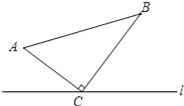
【题目】如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A→C→B路径向终点运动,终点为B点;点Q从B点出发沿B→C→A路径向终点运动,终点为A点.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.设运动时间为t秒,则当t=_________秒时,△PEC与△QFC全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
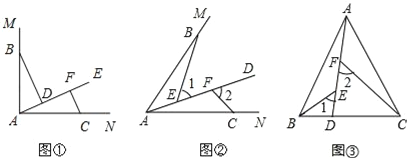
【题目】(1)如图1,∠MAN=90°,射线AE在这个角的内部,点B、C分别在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证:△ABD≌△CAF;
(2)如图2,点B、C分别在∠MAN的边AM、AN上,点E、F都在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,且∠1=∠2=∠BAC.求证:△ABE≌△CAF;
(3)如图3,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,求△ACF与△BDE的面积之和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com