
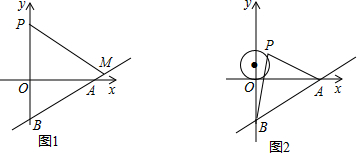
���� ��1�������A��B�������꣬���OA��OB���ù��ɶ������ɽ�����⣮
��2�����ݴ��߶���̣��������M���꣬�����������빫ʽ���㼴�ɣ�
��3����C��CM��AB��M������AC��MC���ӳ��߽���C��N�����������������ʽ�ã�$\frac{1}{2}$��AB��CM=$\frac{1}{2}$��OA��BC����֪ԲC�ϵ㵽ֱ��y=$\frac{3}{4}$x-3����������1+$\frac{16}{5}$=$\frac{21}{5}$��ԲC�ϵ㵽ֱ��y=$\frac{3}{4}$x-3����С������ $\frac{16}{5}$-1=$\frac{11}{5}$���ɴ˼��ɽ�����⣮
��4��������ֱ��y=$\frac{4}{3}$x+1�������ύ��A��0��1����B��-$\frac{3}{4}$��0����ֱ��y=$\frac{4}{3}$x+b��y�ύ�ڵ�P����PM��AB��M���ɡ�ABO�ס�APM����$\frac{PM}{BO}$=$\frac{AP}{AB}$����ΪAB=$\sqrt{{1}^{2}+��\frac{3}{4}��^{2}}$=$\frac{5}{4}$������$\frac{3}{\frac{3}{4}}$=$\frac{PA}{\frac{5}{4}}$���Ƴ�PA=5���Ƴ���P����Ϊ��0��-4����b=-4�����ݶԳ��Կ�֪����b=6ʱ��Ҳ����������
��� �⣺��1����ֱ��y=$\frac{3}{4}$x-3��x�ᡢy��ֱ���A��B���㣬
��A���������4��0����B���������0��-3����
��OA=4��OB=3��
��AB=$\sqrt{{3}^{2}+{4}^{2}}$=5��
��2����ֱ��AB�Ľ���ʽΪy=$\frac{3}{4}$x-3��
�����P��0��4����ֱAB��ֱ�ߵĽ���ʽΪy=-$\frac{4}{3}$x+4��
��$\left\{\begin{array}{l}{y=\frac{3}{4}x-3}\\{y=-\frac{4}{3}x+4}\end{array}\right.$���$\left\{\begin{array}{l}{x=\frac{84}{25}}\\{y=-\frac{12}{25}}\end{array}\right.$��
���ݴ��߶���̿�֪��M����Ϊ��$\frac{84}{25}$��-$\frac{12}{25}$��ʱ��PM��̣���ʱPM=$\sqrt{��\frac{84}{25}��^{2}+��4+\frac{12}{25}��^{2}}$=$\frac{28}{5}$��
��3����C��CM��AB��M������AC��MC���ӳ��߽���C��N��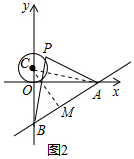
���������������ʽ�ã�$\frac{1}{2}$��AB��CM=$\frac{1}{2}$��OA��BC��
��5��CM=16��
��CM=$\frac{16}{5}$��
��ԲC�ϵ㵽ֱ��y=$\frac{3}{4}$x-3����������1+$\frac{16}{5}$=$\frac{21}{5}$��
���PAB��������ֵ�� $\frac{1}{2}$��5��$\frac{21}{5}$=$\frac{21}{2}$��
ԲC�ϵ㵽ֱ��y=$\frac{3}{4}$x-3����С������ $\frac{16}{5}$-1=$\frac{11}{5}$��
���PAB�������Сֵ�� $\frac{1}{2}$��5��$\frac{11}{5}$=$\frac{11}{2}$��
���PAB�������Сֵ�����ֵ֮��=$\frac{21}{2}$+$\frac{11}{2}$=16��
�ʴ�Ϊ16��
��4����ͼ3�У�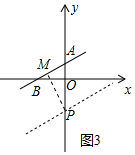
�߲�����ֱ��y=$\frac{4}{3}$x+1�������ύ��A��0��1����B��-$\frac{3}{4}$��0����ֱ��y=$\frac{4}{3}$x+b��y�ύ�ڵ�P����PM��AB��M��
�ߡ�ABO�ס�APM��
��$\frac{PM}{BO}$=$\frac{AP}{AB}$����AB=$\sqrt{{1}^{2}+��\frac{3}{4}��^{2}}$=$\frac{5}{4}$��
��$\frac{3}{\frac{3}{4}}$=$\frac{PA}{\frac{5}{4}}$��
��PA=5��
���P������0��-4����
��b=-4��
���ݶԳ��Կ�֪����b=6ʱ��Ҳ����������
�ʴ�Ϊ-4��6��
���� ���⿼��һ�κ�����Ӧ�á������ε���������������ε��ж������ʡ��㵽ֱ�ߵľ��빫ʽ��Ӧ�ã������Ĺؼ������Բ�ϵĵ㵽ֱ��AB���������Լ���С���ۣ�ѧ���÷������۵�˼��˼�����⣬�����п�ѹ���⣮


 ���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com