
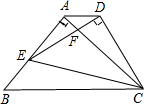
 如图,△ABC为等腰直角三角形,∠BAC=90°,BC=1,E为直角边AB上任意一点,以线段CE为斜边作等腰Rt△CDE,连接AD,下列说法:①AC⊥ED;②∠BCE=∠ACD;③△AED∽△ECB;④AD∥BC;⑤四边形ABCD面积的最大值为$\frac{3}{8}$,其中正确的是②④⑤.
如图,△ABC为等腰直角三角形,∠BAC=90°,BC=1,E为直角边AB上任意一点,以线段CE为斜边作等腰Rt△CDE,连接AD,下列说法:①AC⊥ED;②∠BCE=∠ACD;③△AED∽△ECB;④AD∥BC;⑤四边形ABCD面积的最大值为$\frac{3}{8}$,其中正确的是②④⑤. 分析 由三角形ABC与三角形ECD都为等腰直角三角形,利用等腰直角三角形的性质得到AB=AC,CD=DE,且四个锐角为45°,利用等式的性质得到∠BCE=∠ACD,故选项②正确;根据B与E重合时,A与D重合,此时DE与AC垂直;当B,E不重合时,A,D也不重合,根据∠BAC与∠EDC都为直角,判断∠AFE与∠DFC是否锐角,即可对于选项①做出判断;由两边对应成比例且夹角相等的三角形相似得到三角形BEC与三角形ADC相似,利用相似三角形对应角相等及等式的性质得到一对内错角相等,利用内错角相等两直线平行得到AD与BC平行,可得出选项④正确;由④的结论判断选项③即可;根据△ABC的面积为定值,若梯形ABCD的面积最大,则△ACD的面积最大;由高一定,面积最大即为AD最长,故梯形ABCD面积最大时,E、A重合,求出此时面积,即为最大面积,即可对于选项⑤做出判断.
解答 解:∵△ABC,△ECD都为等腰直角三角形,
∴AB=AC=$\frac{\sqrt{2}}{2}$BC=$\frac{\sqrt{2}}{2}$,CD=DE=$\frac{\sqrt{2}}{2}$CE,∠B=∠ACB=∠DCE=∠DEC=45°,
∴∠ACB-∠ACE=∠DCE-∠ACE,即∠BCE=∠ACD,故选项②正确;
当B,E重合时,A,D重合,此时DE⊥AC;
当B,E不重合时,A,D也不重合,由∠BAC与∠EDC都为直角,得到∠AFE与∠DFC必为锐角,故①错误;
④∵$\frac{CD}{EC}$=$\frac{AC}{BC}$=$\frac{\sqrt{2}}{2}$,
∴$\frac{CD}{AC}$=$\frac{CE}{BC}$,
由①知∠ECB=∠DCA,
∴△BEC∽△ADC;
∴∠DAC=∠B=45°;
∴∠DAC=∠BCA=45°,即AD∥BC,故④正确;
③∵由④知∠DAC=45°,
∴∠EAD=135°,∠BEC=∠EAC+∠ECA=90°+∠ECA;
∵∠ECA<45°,
∴∠BEC<135°,即∠BEC<∠EAD;
∴△EAD与△BEC不相似,故③错误;
⑤∵△ABC的面积为定值,
∴若梯形ABCD的面积最大,则△ACD的面积最大;
∵△ACD中,AD边上的高为定值,
∴若△ACD的面积最大,则AD的长最大;
由④的△BEC∽△ADC知:当AD最长时,BE也最长;
故梯形ABCD面积最大时,E、A重合,此时EC=AC=$\frac{\sqrt{2}}{2}$,AD=$\frac{1}{2}$;
故S梯形ABCD=$\frac{1}{2}$(1+$\frac{1}{2}$)×$\frac{1}{2}$=$\frac{3}{8}$,故⑤正确.
故答案为:②④⑤.
点评 此题属于相似形综合题,涉及的知识有:相似三角形的判定与性质,等腰直角三角形的性质,平行线的判定与性质,熟练掌握相似三角形的判定与性质是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
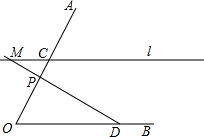 如图,已知C、D分别是∠AOB的边OA和OB上两个定点,过点C的直线ι∥OB,P是边OA上的一个动点,射线DP交直线l于点M,tan∠AOB=2,l与OB的距离等于6,OD=10.
如图,已知C、D分别是∠AOB的边OA和OB上两个定点,过点C的直线ι∥OB,P是边OA上的一个动点,射线DP交直线l于点M,tan∠AOB=2,l与OB的距离等于6,OD=10.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
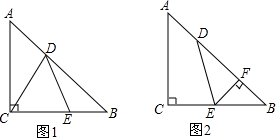
 如图,在△ABC中,∠C=90°,AC=BC,点D在BC边上,连接AD,将AD绕点D顺时针旋转90°得到DE,连接BE,作DF⊥BC交AB于点F.
如图,在△ABC中,∠C=90°,AC=BC,点D在BC边上,连接AD,将AD绕点D顺时针旋转90°得到DE,连接BE,作DF⊥BC交AB于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
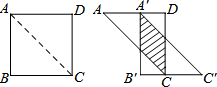 如图,将边长为12cm的正方形纸片ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分(见图中阴影)的面积为32cm2,则它移动的距离AA′等于( )
如图,将边长为12cm的正方形纸片ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分(见图中阴影)的面积为32cm2,则它移动的距离AA′等于( )| A. | 6cm | B. | 8cm | C. | 6cm或8cm | D. | 4cm或8cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com