
【题目】已知AB=10cm,点C在直线AB上,如果BC=4cm,点D是线段AC的中点,求线段BD的长度.
【答案】7cm或3cm
【解析】
根据C点在直线AB上的位置分类讨论①当C点在线段AB间时,先算出AC的长,再根据D为AC中点,计算出CD的长,最后计算BC+CD即可;②当C在线段AB外时,先计算AC的长,再根据中点算出CD的长,最后计算CD-BC即可.
(1)当C在线段AB间时
∵AB=10,边长、BC=4cm
∴AC=6cm
又∵点D是AC的中点,
所以AD=CD=![]() AC=3cm,
AC=3cm,
∵D是AC的中点,
∴CD=![]() AC=3cm
AC=3cm
BD=BC+CD=4+3=7cm
(2)当C在线段AB外时,
∵BC=4,AB=10
∴AC=14
∵D时AC的中点,
CD=![]() AC=7cm
AC=7cm
BD=CD-BC=7-4=3cm
故答案是:7cm或3cm


科目:初中数学 来源: 题型:
【题目】某县为了更好保障居民饮用水安全,环保局决定购10台污水处理设备,现有A、B两种型号的设备,价格与每台日处理污水的能力见下表.

(1)若县环保局购买污水处理设备的资金不超过105万元,你认为有哪几种方案.
(2)在(1)的条件下,每日要求处理污水量不低于2040吨,为了节约资金,请设计“一个最省钱”的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,矩形OABC在平面直角坐标系内的位置如图所示,点O为坐标原点,点A的坐标为(10,0),点B的坐标为(10,8),已知直线AC与双曲线y=![]() (m≠0)在第一象限内有一交点Q(5,n).
(m≠0)在第一象限内有一交点Q(5,n).
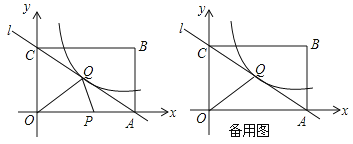
(1)求直线AC和双曲线的解析式;
(2)若动点P从A点出发,沿折线AO→OC的路径以每秒2个单位长度的速度运动,到达C处停止.求△OPQ的面积S与的运动时间t秒的函数关系式,并求当t取何值时S=10.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“滴滴快车”是一种便捷的出行工具,计价规则如下表:
计费项目 | 里程费 | 时长费 |
单价 | 1.4元/千米 | 0.5元/分钟 |
注:车费由里程费、时长费两部分构成,其中里程费按行车的实际里程计费,时长费按行车的实际时间计算。车费不足8元的按最低消费8元收取。为了推广和扩大“滴滴快车”的市场占有率,公司近期推出优惠政策,凡车费满10元,将给予8折优惠。 | ||
随着互联网的不断发展,更多的人们选择了“滴滴快车”出行。假设“滴滴快车”的平均行车速度为50 km/h,请回答下列问题:
(1)小明和小冰各自乘坐“滴滴快车”,行车里程分别为3千米和10千米,请问他们各自需付车费多少钱?
(2)张老师与王老师的家和学校在同一条直线上,位置如图所示.一天,张老师和王老师各自从学校“滴滴快车”回家,分别付车费9.6元和24元.请问,张老师和王老师的家相距多少千米?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明家的住房结构平面图,(单位:米),装修房子时,他打算将卧室以外的部分都铺上地砖,
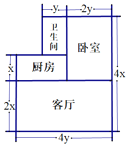
(1)若铺地砖的价格为80元/平方米,那么购买地砖需要花多少钱?(用代数式表示);
(2)已知房屋的高度为3米,现在想要在客厅和卧室的墙壁上贴上壁纸,那么需要多少平方米的壁纸(门窗所占面积忽略不计)?(用代数式表示);
(3)若x=4,y=5,且每平方米地砖的价格是90元,每平方米壁纸的价格是15元,那么,在这两项装修中,小明共要花费多少钱?(各种小的损耗不计).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣.已知购买甲型机器人1台,乙型机器人2台,共需14万元;购买甲型机器人2台,乙型机器人3台,共需24万元.
(1)求甲、乙两种型号的机器人每台的价格各是多少万元;
(2)已知甲型和乙型机器人每台每小时分拣快递分别是1200件和1000件,该公司计划购买这两种型号的机器人共8台,总费用不超过41万元,并且使这8台机器人每小时分拣快递件数总和不少于8300件,则该公司有哪几种购买方案?哪个方案费用最低,最低费用是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以下各图都是由同样大小的图形①按一定规律组成,其中第①个图形中共有1个完整菱形,第②个图形中共有5个完整菱形,第③个图形中共有13个完整菱形,…,则第⑦个图形中完整菱形的个数为( )

A. 83B. 84C. 85D. 86
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=8,AD=12,M是AD边的中点,P是AB边上的一个动点(不与A、B重合),PM的延长线交射线CD于Q点,MN⊥PQ交射线BC于N点。
(1)若点N在BC之间时,如图:
①求证:∠NPQ=∠PQN;
②请问![]() 是否为定值?若是定值,求出该定值;若不是,请举反例说明;
是否为定值?若是定值,求出该定值;若不是,请举反例说明;
(2)当△PBN与△NCQ的面积相等时,求AP的值.
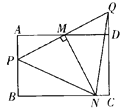
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com