
【题目】某县为了更好保障居民饮用水安全,环保局决定购10台污水处理设备,现有A、B两种型号的设备,价格与每台日处理污水的能力见下表.

(1)若县环保局购买污水处理设备的资金不超过105万元,你认为有哪几种方案.
(2)在(1)的条件下,每日要求处理污水量不低于2040吨,为了节约资金,请设计“一个最省钱”的购买方案.
【答案】(1)①购买10台B型;②购买1台A型和9台B型;③购买2台A型和8台B型.(2)购买1台A型和9台B型的方案满足要求;
【解析】
(1)设应购置A型号的污水处理设备x台,则购置B型号的污水处理设备(10-x)台,由于要求资金不能超过105,即购买资金12x+10(10-x)应小于等于105,由此求出关于A型号处理机购买的几种方案;
(2)由(1)得出的方案进行分类讨论,既满足得到每月要求处理的污水量不低于2040吨且又节约资金,选择符合题意得那个方案即可.
解:(1)设购买A型设备x台,则B型设备(10﹣x)台,依题意得,
12x+10(10﹣x)≤105 …
解得,x≤2.5;…
又x取自然数(或说非负整数),故x=2,1,0 …
所以,符合要求的购买方案有以下3种:
①购买10台B型;②购买1台A型和9台B型;③购买2台A型和8台B型.
(2)法一:分别计算每种方案的资金及污水处理能力如下:
①购买10台B型:费用10×10=100万元;污水处理200×10=2000吨
②购买1台A型和9台B型:费用12+9×10=102万元;污水处理240+200×9=2040吨
③购买2台A型和8台B型:费用12×2+8×10=104万元;
故购买1台A型和9台B型的方案满足要求…
方法二:设购买A型设备x台,则B型设备(10﹣x)台,由题意得:
240x+200×(10﹣x)≥2040,
解得,x≥1,
由生活实际可知价格便宜的购置数量越多越省钱,故购买1台A型和9台B型符合要求,


科目:初中数学 来源: 题型:
【题目】一件商品的包装盒是一个长方体(如图1),它的宽和高相等.小明将四个这样的包装盒放入一个长方体大纸箱中,从上面看所得图形如图2所示,大纸箱底面长方形未被覆盖的部分用阴影表示.接着小明将这四个包装盒又换了一种摆放方式,从上面看所得图形如图3所示,大纸箱底面未被覆盖的部分也用阴影表示.
设图1中商品包装盒的宽为a,则商品包装盒的长为___________,图2中阴影部分的周长与图3中阴影部分的周长的差为____________(都用含a的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() (1,0)和点
(1,0)和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,对称轴为直线
,对称轴为直线![]() =1.
=1.
(1)求点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示)
的代数式表示)
(2)连接![]() 、
、![]() ,若△
,若△![]() 的面积为6,求此抛物线的解析式;
的面积为6,求此抛物线的解析式;
(3)在(2)的条件下,点![]() 为
为![]() 轴正半轴上的一点,点
轴正半轴上的一点,点![]() 与点
与点![]() ,点
,点![]() 与点
与点![]() 关于点
关于点![]() 成中心对称,当△
成中心对称,当△![]() 为直角三角形时,求点
为直角三角形时,求点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮房间窗户的窗帘如图1所示,它是由两个四分之一圆组成(半径相同)
(1)用代数式表示窗户能射进阳光的面积是 .(结果保留π)
(2)当![]() ,b=1时,求窗户能射进阳光的面积是多少?(取π≈3)
,b=1时,求窗户能射进阳光的面积是多少?(取π≈3)
(3)小亮又设计了如图2的窗帘(由一个半圆和两个四分之一圆组成,半径相同),请你帮他算一算此时窗户能射进阳光的面积是否更大?如果更大,那么大多少?(结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,点A的坐标为A(-1,0).
(1)画出△ABC平移后得到的![]() 使得点A的对应点
使得点A的对应点![]() 的坐标为(2,-1),并写出
的坐标为(2,-1),并写出![]() 的坐标;
的坐标;
(2)画出△ABC绕点A顺时针旋转90°后得到的![]() 写出
写出![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知12箱苹果,以每箱10千克为标准,超过10千克的数记为正数,不足10千克的数记为负数,称重记录如下:
+0.2 ,—0.2,+0. 7,—0.3,—0.4,+0.6,0,—0.1,—0.6,+0.5,—0.2,—0.5。
⑴求12箱苹果的总重量;
⑵若每箱苹果的重量标准为10![]() 0.5(千克),则这12箱有几箱不合乎标准的?
0.5(千克),则这12箱有几箱不合乎标准的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在查阅大数学家高斯的资料时,知道了高斯如何求1+2+3+…+100.小明于是对从1开始连续奇数的和进行了研究,发现如下式子:
第1个等式: ![]() ;第2个等式:
;第2个等式: ![]() ;第3个等式:
;第3个等式: ![]()
探索以上等式的规律,解决下列问题:
(1) ![]()
![]()
![]() ;
;
(2)完成第![]() 个等式的填空:
个等式的填空: ![]() ;
;
(3)利用上述结论,计算51+53+55+…+109 .
查看答案和解析>>
科目:初中数学 来源: 题型:
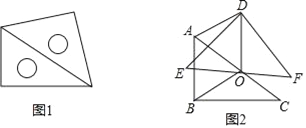
【题目】如图1,放置的一副三角尺,将含45°角的三角尺斜边中点O为旋转中心,逆时针旋转30°得到如图2,连接OB、OD、AD.
(1)求证:△AOB≌△AOD;
(2)试判定四边形ABOD是什么四边形,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com