
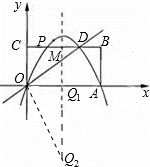
矩形OABC在直角坐标系中的位置如图所示,A、C两点的坐标分别为A(6,0)、C(0,3),直线y=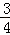 x与BC边相交于点D.
x与BC边相交于点D.
(1)求点D的坐标;
(2)若抛物线y=ax2+bx经过D、A两点,试确定此抛物线的表达式;
(3)P为x轴上方(2)中抛物线上一点,求△POA面积的最大值;
(4)设(2)中抛物线的对称轴与直线OD交于点M,点Q为对称轴上一动点,以Q、O、M为顶点的三角形与△OCD相似,求符合条件的Q点的坐标.

解:(1)由题知,直线y=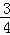 x与BC交于点D(x,3).(1分)
x与BC交于点D(x,3).(1分)
把y=3代入y=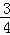 x中得,x=4,
x中得,x=4,
∴D(4,3);(3分)
(2)抛物线y=ax2+bx经过D(4,3)、A(6,0)两点,分别代入y=ax2+bx中,(4分)
得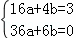
解之得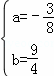 (5分)
(5分)
∴抛物线的解析式为y=﹣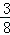 x2+
x2+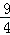 x;(6分)
x;(6分)
(3)因△POA底边OA=6,
∴当S△POA有最大值时,点P须位于抛物线的最高点,
∵a=﹣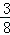 <0,
<0,
∴抛物线顶点恰为最高点,(7分)
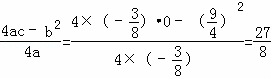 (8分)
(8分)
∴S△POA的最大值= ×6×
×6×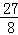 =
=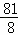 ;(10分)
;(10分)
(4)抛物线的对称轴与x轴交于点Q1,符合条件.
∵CB∥OA,∠Q1OM=∠CDO,
∴Rt△Q1OM∽Rt△CDO.x=﹣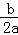 =3,该点坐标为Q1(3,0).(11分)
=3,该点坐标为Q1(3,0).(11分)
过点O作OD的垂线交抛物线的对称轴于点Q2,
∵对称轴平行于y轴,
∴∠Q2MO=∠DOC,
∴Rt△Q2MO∽Rt△DOC.
在Rt△Q2Q1O和Rt△DCO中
Q1O=CO=3,∠Q2=∠ODC,
∴Rt△Q2Q1O≌Rt△DCO.
∴CD=Q1Q2=4,
∵点Q2位于第四象限,
∴Q2(3,﹣4).(12分)
因此,符合条件的点有两个,分别是Q1(3,0),Q2(3,﹣4).(13分)


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②a+b+c>0;③4a+2b+c<0;④b<a+c;⑤b2﹣4ac>0,其中正确的结论有 .(只填序号)
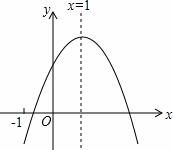
查看答案和解析>>
科目:初中数学 来源: 题型:
“初中生骑电动车上学”的现象越来越受到社会的关注,某校利用“五一”假期,随机抽查了本校若干名学生和部分家长对“初中生骑电动车上学”现象的看法,统计整理制作了如下的统计图,请回答下列问题:
(1)这次抽查的家长总人数为 ;
(2)请补全条形统计图和扇形统计图;
(3)从这次接受调查的学生中,随机抽查一个学生恰好抽到持“无所谓”态度的概率是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,为估算某河的宽度,在河对岸选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20m,CE=10m,CD=20m,则河的宽度AB等于( )

A. 60m B. 40m C. 30m D. 20m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com