
【题目】已知线段AB⊥直线l于点B,点M在直线l上,分别以AB、AM为边作等边△ABC和等边△AMN,直线CN交直线l于点D.
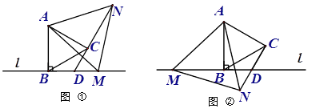
(1)当点M在AB右侧时,如图①,试探索线段CN、CD、DM的数量关系,并说明理由;
(2)当点M在AB左侧时,如图②,(1)中线段CN、CD、DM的数量关系仍然成立吗?若不成立,写出新的数量关系;
(3)若BM=2BD,DN=9,则CD= .
【答案】(1)MD=CN-CD;理由见解析;
(2)(1)中的数量关系不成立,MD=CN+CD;理由见解析;
(3)CD=3或9
【解析】
(1)如图①中,设AM交ND于O.首先证明△ABM≌△ACN(SAS),推出BM=NC,再证明BD=CD即可得到MD=CN-CD;
(2)如图②, 设AM交ND于O.类似(1)的证明方法,先证明△ABM≌△ACN(SAS),得到CN=BM,再证明CD=BD,可得到MD=CN+CD;
(3)分图①,图②两种情形,设BD=CD=x,则BM=2x,列出方程分别求解即可.
(1)MD=CN-CD;理由是:
如图①中,设AM交ND于O.
∵△ABC,△AMN都是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAM=∠CAN,
∴△ABM≌△ACN(SAS),
∴CN=BM,
∴∠ANO=∠DMO,
∵∠AON=∠DOM,
∴∠ODM=∠OAN=60°,
∵AB⊥BC,
∴∠ABM=90°,
∵∠ABC=60°,
∴∠CBD=30°,
∵∠ODM=∠CBD+∠BCD,
∴∠DBC=∠DCB=30°,
∴CD=BD,
∴MD=CN-CD
(2)不成立,MD=CN+CD;
证明:如图②, 设AM交ND于O.

∵△ABC,△AMN都是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAM=∠CAN,
∴△ABM≌△ACN(SAS),
∴CN=BM,
∴∠ANC=∠AMB,
∵∠AOM=∠DON,
∴∠ODN=∠OAM=60°,
∵AB⊥BD,
∴∠ABD=90°,
∵∠ABC=60°,
∴∠CBD=30°,
∵∠ODN=∠CBD+∠BCD,
∴∠DBC=∠DCB=30°,
∴CD=BD,
∴MD=MB+BD=CN+CD;
(3)分两种情况:
①如图①中,

∵BM=2BD,设BD=MD=CD=x,则BM=2x,
∵DN=9,BM=NC,
∴BM+CD=DN
∴2x+x=9,
∴x=3
∴CD=3.
②如图②中,设BD=CD=x,则BM=2x,

∵BM=NC,ND=9,
CD+DN= CN;
∴x+9=2x,
∴x=9,
∴CD=9,
综上所述,CD=3或9.
故答案为3或9.


科目:初中数学 来源: 题型:
【题目】西瓜经营户以2元/千克的价格购进一批小型西瓜,以3元/千克的价格出售,每天可售出200千克.为了促销,该经营户决定降价销售.经调查发现,这种小型西瓜每降价0.1元/千克,每天可多售出40千克.另外,每天的房租等固定成本共24元,为了减少库存,该经营户要想每天盈利200元,应将每千克小型西瓜的售价降低( )元.
A.0.2或0.3
B.0.4
C.0.3
D.0.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将长方形纸片ABCD沿过点B的直线折叠,使点A落在BC边上点F处,折痕为BE,再沿过点E的直线折叠,使点D落在BE边上点D’处,折痕为EG,展平纸片,则图中∠FEG= ______ °
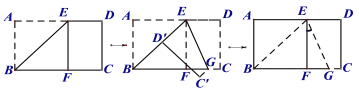
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,正方形
中,正方形![]() 中心在原点,且顶点
中心在原点,且顶点![]() 的坐标为
的坐标为![]() .动点
.动点![]() 分别从点
分别从点![]() 同时出发,绕着正方形的边按顺时针方向运动,当
同时出发,绕着正方形的边按顺时针方向运动,当![]() 点回到
点回到![]() 点时两点同时停止运动,运动时间为
点时两点同时停止运动,运动时间为![]() 秒.连接
秒.连接![]() ,线段
,线段![]() 、
、![]() 与正方形的边围成的面积较小部分的图形记为
与正方形的边围成的面积较小部分的图形记为![]() .
.
(1)请写出![]() 点的坐标.
点的坐标.
(2)若![]() 的速度均为1个单位长度秒,试判断在运动过程中,
的速度均为1个单位长度秒,试判断在运动过程中,![]() 的面积是否发生变化,如果不变求出该值,如果变化说明理由.
的面积是否发生变化,如果不变求出该值,如果变化说明理由.
(3)若![]() 点速度为2个单位长度秒,
点速度为2个单位长度秒,![]() 点为1个单位长度/秒,当
点为1个单位长度/秒,当![]() 的面积为
的面积为![]() 时,求
时,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在数学实践课中测量路灯的高度.如图,已知他的目高![]() 为1.5米,他先站在
为1.5米,他先站在![]() 处看路灯顶端
处看路灯顶端![]() 的仰角为
的仰角为![]() ,向前走3米后站在
,向前走3米后站在![]() 处,此时看灯顶端
处,此时看灯顶端![]() 的仰角为
的仰角为![]() (
(![]() ),则灯顶端
),则灯顶端![]() 到地面的距离约为( )
到地面的距离约为( )
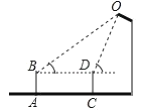
A.3.2米B.4.1米C.4.7米D.5.4米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,BE=CF.
求证:(1)△BDE≌△CDF;
(2)AD是△ABC的角平分线.
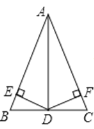
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下表,方程1、方程2、方程3…是按照一定规律排列的一列方程。
(1)猜想方程1的解,并将它们的解填在表中的空白处。
序号 | 方程 | 方程的解( |
1 |
|
|
2 |
|
|
3 |
|
|
… | …… | …… |
(2)若方程![]()
![]() 的解是
的解是![]() ,猜想a,b的值。
,猜想a,b的值。
(3)请写出这列方程中的第n个方程和它的解。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A1,A2,A3,…,An是x轴上的点,且OA1=A1A2=A2A3=A3A4=…=An-1An=1,分别过点A1,A2,A3,…,An作x轴的垂线交二次函数y=![]() x2(x>0)的图象于点P1,P2,P3,…,Pn.若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3……依次进行下去,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn=( )
x2(x>0)的图象于点P1,P2,P3,…,Pn.若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3……依次进行下去,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn=( )
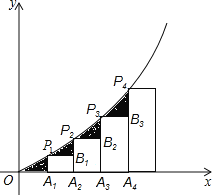
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com