
两个大小不同的等腰直角三角形三角板如图①所示放置,图②是由它抽象出的几何图形,B、C、E在同一条直线上,连结DC.

(1)请找出图②中的全等三角形,并给予说明(说明:结论中不得含有未标识的字母);
(2)试说明:DC⊥BE.
(1)△BAE≌△CAD,理由见解析;(2)证明见解析.
【解析】
试题分析:①可以找出△BAE≌△CAD,条件是AB=AC,DA=EA,∠BAE=∠DAC=90°+∠CAE.
②由①可得出∠DCA=∠ABC=45°,则∠BCD=90°,所以DC⊥BE.
试题解析:①∵△ABC,△DAE是等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°.
∠BAE=∠DAC=90°+∠CAE,
在△BAE和△DAC中

∴△BAE≌△CAD(SAS).
②由①得△BAE≌△CAD.
∴∠DCA=∠B=45°.
∵∠BCA=45°,
∴∠BCD=∠BCA+∠DCA=90°,
∴DC⊥BE.
考点:1.等腰直角三角形;2.全等三角形的判定与性质;3.等腰三角形的判定与性质.


科目:初中数学 来源:2014-2015学年江苏省八年级上学期期中数学试卷(解析版) 题型:解答题
(本题满分10分)
【问题提出】学习了三角形全等的判定方法(即“SAS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
【初步思考】我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.
【深入探究】
第一种情况:当∠B是直角时,△ABC≌△DEF.
(1)如图①,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E=90°,根据 ,可以知道Rt△ABC≌Rt△DEF.
第二种情况:当∠B是钝角时,△ABC≌△DEF.
(2)如图②,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B.∠E都是钝角,求证:△ABC≌△DEF.
第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
(3)在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B.∠E都是锐角,请你用尺规在图③中作出△DEF,使△DEF和△ABC不全等.(不写作法,保留作图痕迹)
(4)∠B还要满足什么条件,就可以使△ABC≌△DEF?请直接写出结论:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B.∠E都是锐角,若 ,则△ABC≌△DEF.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省八年级上学期期中数学试卷(解析版) 题型:选择题
下列四组数据,能作为直角三角形的三边长的是( )
A.2、4、6 B.2、3、4 C.5、7、12 D.8、15、17
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏盐城东台苏东双语学校初二上第一次检测二数学卷(解析版) 题型:解答题
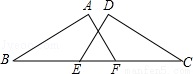
如图,点E、F在BC上,BE=FC,AB=DC,∠B=∠C.求证:∠A=∠D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏盐城东台苏东双语学校初二上第一次检测二数学卷(解析版) 题型:填空题
如图, 已知:BD是∠ABC的平分线,DE⊥BC于E,S△ABC=36cm2;,AB=12cm,BC=18cm则 DE的长为 cm。

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏徐州丰县中学八年级上学期第一次质检数学试卷(解析版) 题型:解答题
如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.求证:BC∥EF.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com