
【题目】已知函数y=![]() (x>0)的图象与一次函数y=ax﹣2(a≠0)的图象交于点A(3,n).
(x>0)的图象与一次函数y=ax﹣2(a≠0)的图象交于点A(3,n).
(1)求实数a的值;
(2)设一次函数y=ax﹣2(a≠0)的图象与y轴交于点B,若点C在y轴上,且S△ABC=2S△AOB,求点C的坐标.
【答案】(1)a=1;(2)C(0,﹣4)或(0,0).
【解析】
(1)把 A(3,n)代入y=![]() (x>0)求得 n 的值,即可得A点坐标, 再把A点坐标代入一次函数 y=ax﹣2 可得 a 的值;(2)先求出一次函数 y=ax﹣2(a≠0)的图象与 y 轴交点 B 的坐标,再分两种情况(①当C点在y轴的正半轴上或原点时;②当C点在y轴的负半轴上时)求点C的坐标即可.
(x>0)求得 n 的值,即可得A点坐标, 再把A点坐标代入一次函数 y=ax﹣2 可得 a 的值;(2)先求出一次函数 y=ax﹣2(a≠0)的图象与 y 轴交点 B 的坐标,再分两种情况(①当C点在y轴的正半轴上或原点时;②当C点在y轴的负半轴上时)求点C的坐标即可.
(1)∵函数 y=![]() (x>0)的图象过(3,n),
(x>0)的图象过(3,n),
∴3n=3,
n=1,
∴A(3,1)
∵一次函数 y=ax﹣2(a≠0)的图象过点 A(3,1),
∴1=3a﹣1, 解得 a=1;
(2)∵一次函数y=ax﹣2(a≠0)的图象与 y 轴交于点 B,
∴B(0,﹣2),
①当C点在y轴的正半轴上或原点时, 设 C(0,m),
∵S△ABC=2S△AOB,
∴![]() ×(m+2)×3=2×
×(m+2)×3=2×![]() ×3, 解得:m=0,
×3, 解得:m=0,
②当C点在 y 轴的负半轴上时, 设(0,h),
∵S△ABC=2S△AOB,
∴![]() ×(﹣2﹣h)×3=2×
×(﹣2﹣h)×3=2×![]() ×3, 解得:h=﹣4,
×3, 解得:h=﹣4,
∴C(0,﹣4)或(0,0).


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.在△ABC外有一点F,使FA⊥AE,FC⊥BC.
(1)求证:BE=CF;
(2)在AB上取一点M,使BM=2DE,连接MC,交AD于点N,连接ME.求证:①ME⊥BC;②DE=DN.

查看答案和解析>>
科目:初中数学 来源: 题型:
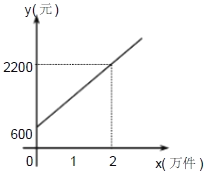
【题目】某公司市场营销部的营销员有部分收入按照业务量或销售额提成,即多卖多得.营销员的月提成收入![]() (元)与其每月的销售量
(元)与其每月的销售量![]() (万件)成一次函数关系,其图象如图所示.根据图象提供的信息,解答下列问题:
(万件)成一次函数关系,其图象如图所示.根据图象提供的信息,解答下列问题:
(1)求出![]() (元)与
(元)与![]() (万件)(其中
(万件)(其中![]() )之间的函数关系式;
)之间的函数关系式;
(2)已知该公司营销员李平12月份的销售量为1.2万件,求李平12月份的提成收入.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为丰富学生的学习生活,某校九年级组织学生参加春游活动,所联系的旅行收费标准如下: 
春游活动结束后,该班共支付给该旅行社活动费用2800元,请问该班共有多少人参加这次春游活动?
查看答案和解析>>
科目:初中数学 来源: 题型:
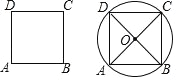
【题目】已知:正方形 ABCD.
求作:正方形 ABCD 的外接圆.
作法:如图,
(1)分别连接 AC,BD,交于点 O;
(2)以点 O 为圆心,OA 长为半径作⊙O,⊙O 即为所求作的圆.
请回答:该作图的依据是__________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系 xOy 中,抛物线 y=ax2﹣4ax+3a﹣2(a≠0)与 x轴交于 A,B 两(点 A 在点 B 左侧).
(1)当抛物线过原点时,求实数 a 的值;
(2)①求抛物线的对称轴;
②求抛物线的顶点的纵坐标(用含 a 的代数式表示);
(3)当 AB≤4 时,求实数 a 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线y=ax2+bx+c与x轴交于A,B两点,与y轴交于正半轴C点,且AC=20,BC=15,∠ACB=90°,则此抛物线的解析式为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
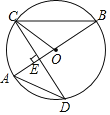
【题目】如图,AB是圆O的直径.CD是⊙O的一条弦.且CD⊥AB于点E.
(1)若∠B=32°,求∠OCE的大小;
(2)若CD=4![]() ,OE=1,求AC的长.
,OE=1,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
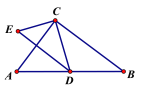
【题目】如图,已知在Rt△ABC与Rt△ECD中,∠ACB=∠ECD=90°,CD为Rt△ABC斜边上的中线,且ED∥BC.
(1)求证:△ABC∽△EDC;
(2)若CE=3,CD=4,求CB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com