
【题目】在平面直角坐标系 xOy 中,抛物线 y=ax2﹣4ax+3a﹣2(a≠0)与 x轴交于 A,B 两(点 A 在点 B 左侧).
(1)当抛物线过原点时,求实数 a 的值;
(2)①求抛物线的对称轴;
②求抛物线的顶点的纵坐标(用含 a 的代数式表示);
(3)当 AB≤4 时,求实数 a 的取值范围.
【答案】(1)a=![]() ;(2)①x=2;②抛物线的顶点的纵坐标为﹣a﹣2;(3)a 的范围为 a<﹣2 或 a≥
;(2)①x=2;②抛物线的顶点的纵坐标为﹣a﹣2;(3)a 的范围为 a<﹣2 或 a≥![]() .
.
【解析】
(1)把原点坐标代入 y=ax2﹣4ax+3a﹣2即可求得a的值;(2)①②把抛物线解析式配成顶点式,即可得到抛物线的对称轴和抛物线的顶点的纵坐标;(3)设 A(m,0),B(n,0),利用抛物线与 x 轴的交点问题,则 m、n 为方程 ax2﹣4ax+3a﹣2=0 的两根,利用判别式的意义解得 a>0 或 a<﹣2,再利用根与系数的关系得到 m+n=4,mn=![]() ,然后根据完全平方公式利用 n﹣m≤4 得到(m+n)2﹣4mn≤16,所以 42﹣4
,然后根据完全平方公式利用 n﹣m≤4 得到(m+n)2﹣4mn≤16,所以 42﹣4![]() ≤16,接着解关于a 的不等式,最后确定a的范围.
≤16,接着解关于a 的不等式,最后确定a的范围.
(1)把(0,0)代入 y=ax2﹣4ax+3a﹣2 得 3a﹣2=0,解得 a=![]() ;
;
(2)①y=a(x﹣2)2﹣a﹣2, 抛物线的对称轴为直线 x=2;
②抛物线的顶点的纵坐标为﹣a﹣2;
(3)设 A(m,0),B(n,0),
∵m、n 为方程 ax2﹣4ax+3a﹣2=0 的两根,
∴△=16a2﹣4a(3a﹣2)>0,解得 a>0 或 a<﹣2,
∴m+n=4,mn=![]() , 而 n﹣m≤4,
, 而 n﹣m≤4,
∴(n﹣m)2≤16,即(m+n)2﹣4mn≤16,
∴42﹣4 ![]() ≤16,
≤16,
即![]() ≥0,解得 a≥
≥0,解得 a≥![]() 或 a<0.
或 a<0.
∴a 的范围为 a<﹣2 或 a≥![]() .
.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
(1)求证:BD=CD;
(2)请判断B,E,C三点是否在以D为圆心,以DB为半径的圆上?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】举重比赛的总成绩是选手的挺举与抓举两项成绩之和,若其中一项三次挑战失败,则该项成绩为 0,甲、乙是同一重量级别的举重选手,他们近三年六次重要比赛的成绩如下(单位:公斤):
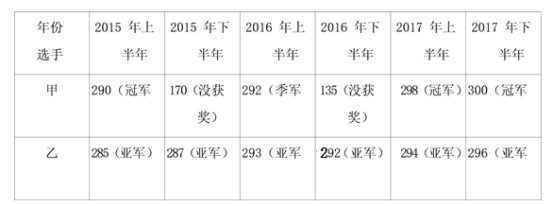
如果你是教练,要选派一名选手参加国际比赛,那么你会选择_____(填“甲” 或“乙”),理由是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=![]() (x>0)的图象与一次函数y=ax﹣2(a≠0)的图象交于点A(3,n).
(x>0)的图象与一次函数y=ax﹣2(a≠0)的图象交于点A(3,n).
(1)求实数a的值;
(2)设一次函数y=ax﹣2(a≠0)的图象与y轴交于点B,若点C在y轴上,且S△ABC=2S△AOB,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象所示,对称轴为x=1,给出下列结论:①abc>0;②当x>2时,y>0;③3a+c>0;④3a+b>0.其中正确的结论有( )

A. ①② B. ①④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,点O是AC上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于E,交∠BCA的外角平分线于F.
(1)请猜测OE与OF的大小关系,并说明你的理由;
(2)点O运动到何处时,四边形AECF是矩形?写出推理过程;
(3)点O运动到何处且△ABC满足什么条件时,四边形AECF是正方形?(写出结论即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
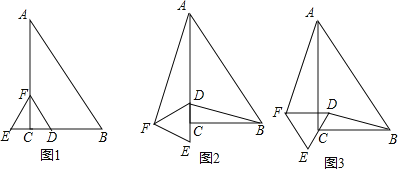
【题目】△ABC中,∠ACB=90°,∠BAC=30°,点C为等边△DEF的边DE的中点.
(1)如图1,当DE与BC在同一条直线上时,已知![]() ,求
,求![]() 的值;
的值;
(2)如图2,当DE与AC在同一条直线上时,分别连接AF,BD,试判断BD和AF的位置关系并说明理由;
(3)如图3,当DE与△ABC的边均不在一条直线上时,分别连接AF,BD,求证:∠FAC=∠CBD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若反比例函数y=![]() (k≠0)的图象过点(2,1),则这个函数的图象还经过的点是( )
(k≠0)的图象过点(2,1),则这个函数的图象还经过的点是( )
A. (﹣2,1) B. (﹣l,2) C. (﹣2,﹣1) D. (1,﹣2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com