
分析 (1)根据平方差公式,可得答案;
(2)根据分母有理化,可得二次根式的加减,根据二次根式的加减,可得答案.
解答 解:(1)规律是($\sqrt{n+1}$+$\sqrt{n}$)($\sqrt{n+1}$-$\sqrt{n}$)=1,得出$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1\sqrt{n}}$.
(2)原式=($\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{2016}$-$\sqrt{2015}$)($\sqrt{2016}$+1)
=($\sqrt{2016}$-1)($\sqrt{2016}$+1)
=2016-1
=2015.
点评 本题考查了分母有理化,利用平方差公式解题关键.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:选择题
| A. | 为了了解一批电视机的使用寿命,采用普查方式 | |
| B. | 为了了解全国中学生的视力状况,采用普查方式 | |
| C. | 对嫦娥三号卫星零部件的检查,采用抽样调查的方式 | |
| D. | 为了了解人们保护水资源的意识,采用抽样调查的方式 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
| 人数变化 (人) | +31 | +178 | -58 | -8 | -1 | -16 | -115 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
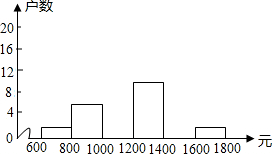 中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如图的频数分布表和频数分布直方图.
中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如图的频数分布表和频数分布直方图. | 分组 | 频数 | 百分比 |
| 600≤x<800 | 2 | 5% |
| 800≤x<1000 | 6 | 15% |
| 1000≤x<1200 | 45% | |
| 9 | 22.5% | |
| 1600≤x<1800 | 2 | |
| 合计 | 40 | 100% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com