
【题目】如图,△ABC中,BC=10,AC-AB=4,AD是∠BAC的角平分线,CD⊥AD,则S△BDC的最大值为( )

A.40B.28C.20D.10
【答案】D
【解析】
如图,延长AB、CD交于E,由AD是角平分线可得∠EAD=∠CAD,利用SAS可证明△EAD≌△CAD,可得AC=AE,CD=DE,可得S△BDC=![]() S△BEC,根据AC-AB=4可得BE=4,当BE⊥BC时,△BEC的面积最大,即可得△BDC的面积.
S△BEC,根据AC-AB=4可得BE=4,当BE⊥BC时,△BEC的面积最大,即可得△BDC的面积.
如图,延长AB、CD交于E,
∵AD是∠BAC的角平分线,CD⊥AD,
∴∠EAD=∠CAD,∠ADE=∠ADC=90°,
在△EAD和△CAD中, ,
,
∴△EAD≌△CAD,
∴AC=AE,CD=DE,
∴S△BDC=![]() S△BEC,
S△BEC,
∵AC-AB=4,
∴AE-AB=4,即BE=4,
当BE⊥BC时△BEC的面积最大,即△BDC的面积最大,
∴S△BDC=![]() ×
×![]() BC·BE=
BC·BE=![]() ×
×![]() ×10×4=10,
×10×4=10,

故选D.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】若等腰三角形腰长为2,有一个内角为80°,则它的底边长上的高为__.(精确到0.01,参考数据:sin50°≈0.766;sin80°≈0.985)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某木板加工厂将购进的A型、B型两种木板加工成C型,D型两种木板出售,已知一块A型木板的进价比一块B型木板的进价少10元,且购买3块A型木板和2块B型木板共花费120元.
(1)A型木板与B型木板的进价各是多少元?
(2)根据市场需求,该木板加工厂决定用不超过2770元购进A型木板、B型木板共100块,若一块A型木板可制成1块C型木板、2块D型木板;一块B型木板可制成2块C型木板、1块D型木板,且生产出来的C型木板数量不少于D型木板的数量的7/5.
①该木板加工厂有几种进货方案?
②若C型木板每块售价30元,D型木板每块售价25元,且生产出来的C型木板、D型木板全部售出,哪一种方案获得的利润最大,求出最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料:
对数的创始人是苏格兰数学家纳皮尔(J.Nplcr,1550-1617年),纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉(Evlcr,1707-1783年)才发现指数与对数之间的联系.
对数的定义:一般地,若ax=N(a>0,a≠1),那么x叫做以a为底N的对数,记作:x=logaN.比如指数式24=16可以转化为4=log216,对数式2=log525可以转化为52=25.
我们根据对数的定义可得到对数的一个性质:loga(MN)=logaM+logaN(a>0,a≠1,M>0,N>0);理由如下:
设logaM=m,logaN=n,则M=am,N=an
∴MN=aman=am+n,由对数的定义得m+n=loga(MN)
又∵m+n=logaM+logaN
∴loga(MN)=logaM+logaN
解决以下问题:
(1)将指数43=64转化为对数式: .
(2)仿照上面的材料,试证明:![]() =
=![]() —
—![]() (a>0,a
(a>0,a![]() l,M>0,N>0).
l,M>0,N>0).
(3) 拓展运用:计算log32+log36-log34=____.
查看答案和解析>>
科目:初中数学 来源: 题型:
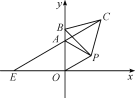
【题目】如图,在平面直角坐标系中,△AOP为等边三角形,A(0,2),点B为y轴上一动点,以BP为边作等边△PBC,延长CA交x轴于点E.
(1)求证:OB=AC;
(2)∠CAP的度数是;
(3)当B点运动时,猜想AE的长度是否发生变化?并说明理由;
(4)在(3)的条件下,在y轴上存在点Q,使得△AEQ为等腰三角形,请写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.∠BAD=60°,AC平分∠BAD,AC=2,BN的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车和一辆摩托车分别从![]() ,
,![]() 两地去同一城市
两地去同一城市![]() ,它们离
,它们离![]() 地的路程随时间变化的图象如图所示,根据图象中的信息解答以下问题:
地的路程随时间变化的图象如图所示,根据图象中的信息解答以下问题:

(1)![]() ,
,![]() 两地相距______
两地相距______![]() ;
;
(2)分别求出摩托车和汽车的行驶速度;
(3)若两图象的交点为![]() ,求点
,求点![]() 的坐标,并指出点
的坐标,并指出点![]() 的实际意义.
的实际意义.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文化用品商店用1 000元购进一批“晨光”套尺,很快销售一空;商店又用1 500元购进第二批该款套尺,购进时单价是第一批的![]() 倍,所购数量比第一批多100套.
倍,所购数量比第一批多100套.
(1)求第一批套尺购进时单价是多少?
(2)若商店以每套4元的价格将这两批套尺全部售出,可以盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.

(1)如图1,当点E在边BC上时,求证DE=EB;
(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;
(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com