
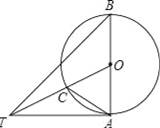
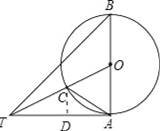
如图,AB是⊙O的直径,∠ABT=45°,AT=AB.
(1)求证:AT是⊙O的切线;
(2)连接OT交⊙O于点C,连接AC,求tan∠TAC.

【考点】切线的判定;解直角三角形.
【专题】证明题.
【分析】(1)根据等腰三角形的性质求得∠TAB=90°,得出TA⊥AB,从而证得AT是⊙O的切线;
(2)作CD⊥AT于D,设OA=x,则AT=2x,根据勾股定理得出OT=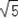
 x,TC=(
x,TC=(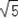
 ﹣1)x,由CD⊥AT,TA⊥AB得出CD∥AB,根据平行线分线段成比例定理得出
﹣1)x,由CD⊥AT,TA⊥AB得出CD∥AB,根据平行线分线段成比例定理得出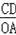
 =
=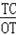
 =
=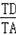
 ,即
,即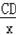
 =
=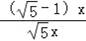
 =
=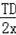
 ,从而求得CD=(1﹣
,从而求得CD=(1﹣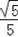
 )x,AD=2x﹣2(1﹣
)x,AD=2x﹣2(1﹣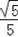
 )x=
)x=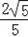
 x,然后解正切函数即可求得.
x,然后解正切函数即可求得.
【解答】解:(1)∵∠ABT=45°,AT=AB.
∴∠TAB=90°,
∴TA⊥AB,
∴AT是⊙O的切线;
(2)作CD⊥AT于D,
∵TA⊥AB,TA=AB=2OA,
设OA=x,则AT=2x,
∴OT=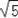
 x,
x,
∴TC=(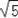
 ﹣1)x,
﹣1)x,
∵CD⊥AT,TA⊥AB
∴CD∥AB,
∴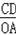
 =
=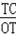
 =
=
 ,即
,即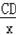
 =
=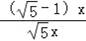
 =
=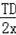
 ,
,
∴CD=(1﹣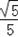
 )x,TD=2(1﹣
)x,TD=2(1﹣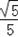
 )x,
)x,
∴AD=2x﹣2(1﹣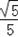
 )x=
)x=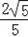
 x,
x,
∴tan∠TAC=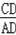
 =
=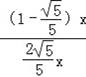
 =
=
 .
.

【点评】本题考查了切线的判定,勾股定理的应用,平行线的判定和性质,解直角三角形等,作出辅助线构建直角三角形是解题的关键.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
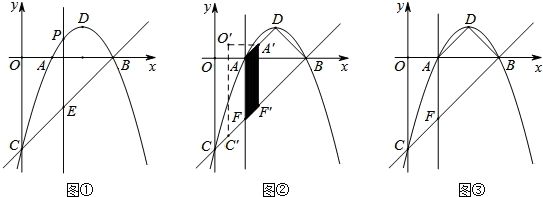
已知二次函数y=ax2+bx+c的图象经过A(1,0),B(3,0),C(0,﹣3)
(1)求此二次函数的解析式以及顶点D的坐标;
(2)如图①,过此二次函数抛物线图象上一动点P(m,n)(0<m<3)作y轴平行线,交直线BC于点E,是否存在一点P,使线段PE的长最大?若存在,求出PE长的最大值;若不存在,说明理由.
(3)如图②,过点A作y轴的平行线交直线BC于点F,连接DA、DB、四边形OAFC沿射线CB方向运动,速度为每秒1个单位长度,运动时间为t秒,当点C与点F重合时立即停止运动,求运动过程中四边形OAFC与四边形ADBF重叠部分面积S的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com