
| A. | 2 | B. | 8 | C. | 10 | D. | 12 |
分析 先求出两根之和与两根之积的值,再将(x1-1)2+(x2-1)2化简成两根之和与两根之积的形式,最后利用二次函数的性质求最小值.
解答 解:∵一元二次方程x2-2ax+a2+a+1=0有两个实根;
∴△=4a2-4×(a2+a+1)=-4(a+1)≥0;
解得:a≤-1;
∵x1,x2是关于x的一元二次方程x2-2ax+a2+a+1=0的两个实根;
∴x1+x2=2a,x1•x2=a2+a+1;
(x1-1)2+(x2-1)2=x12+1-2x1+x22-2x2+1=x12+x22-2(x2+x1)+2
=(x1+x2)2-2x1•x2-2(x1+x2)+2
=4a2-2×(a2+a+1)-2×2a+2
=4a2-2a2-2a-2-4a+2
=2a2-6a
=2(a-$\frac{3}{2}$)2-$\frac{9}{2}$.
故函数y=2(a-$\frac{3}{2}$)2-$\frac{9}{2}$的顶点坐标为($\frac{3}{2}$,-$\frac{9}{2}$),在x=$\frac{3}{2}$的左侧y随x的增大而减小,
∵a≤-1,
∴a=-1时取最小值8.
故选:B.
点评 本题是利用根与系数的关系,把求代数式的最值的问题转化为关于同一个字母的二次三项式的求值问题,从而利用配方法进行判断.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 584×108 | B. | 58.4×109 | C. | 5.84×1010 | D. | 5.84×1011 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
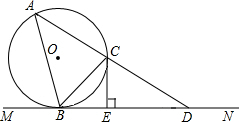 如图所示,MN是⊙O的切线,B为切点,BC是⊙O的弦且∠CBN=45°,过C的直线与⊙O,MN分别交于A,D两点,过C作CE⊥BD于点E.
如图所示,MN是⊙O的切线,B为切点,BC是⊙O的弦且∠CBN=45°,过C的直线与⊙O,MN分别交于A,D两点,过C作CE⊥BD于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 购买商品A的数量 | 购买商品B的数量 | 购买总费用(元) | |
| 第一次购物 | 6 | 5 | 1140 |
| 第二次购物 | 3 | 7 | 1110 |
| 第三次购物 | 9 | 8 | 1128 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com