
分析 (1)由换元的方法可知解题的思想是将复杂问题转化为简单问题解决的思想;
(2)设x2=y,则原方程可化为y2-y-6=0,解之可得y的值,再进一步解关于x的方程可得.
解答 解:(1)在原方程得到方程①的过程中,利用换元法达到降次的目的,体现了转化的数学思想,
故答案为:转化.
(2)设x2=y,则原方程可化为y2-y-6=0.
解得y1=3,y2=-2(不合题意,舍去).
由x2=3可得解是:x1=$\sqrt{3}$,x2=-$\sqrt{3}$,
故方程x4-x2-6=0的解是x1=$\sqrt{3}$,x2=-$\sqrt{3}$.
点评 本题主要考查换元法解方程的方法,我们常用的是整体换元法,是在已知或者未知中,某个代数式几次出现,而用一个字母来代替它从而简化问题,当然有时候要通过变形才能发现.把一些形式复杂的方程通过换元的方法变成一元二次方程,从而达到降次的目的.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
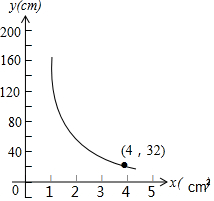 你吃过拉面吗?实际上在制作拉面的过程中就渗透着数学知识,一定体积的面团做拉面,面条的总长度y(cm)与面条的粗细(横截面积)x(cm2)的关系如图所示:
你吃过拉面吗?实际上在制作拉面的过程中就渗透着数学知识,一定体积的面团做拉面,面条的总长度y(cm)与面条的粗细(横截面积)x(cm2)的关系如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com