
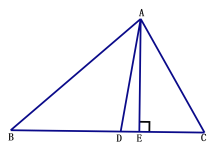
【题目】如图,AD、AE分别是△ABC的角平分线和高线.
(1) 若∠B=50°,∠C=60°,求∠DAE的度数;
(2)若∠C >∠B,猜想∠DAE与∠C-∠B之间的数量关系,并加以证明.
【答案】(1)5°;(2)∠ DAE =![]() (∠C-∠B). 证明见解析。
(∠C-∠B). 证明见解析。
【解析】
(1)先根据三角形内角和得到∠CAB=180°-∠B-∠C=70°,再根据角平分线与高线的定义得到∠CAD=![]() ∠CAB=35°,∠AEC=90°,则∠CAE=90°-∠C=30°,然后利用∠DAE=∠CAD-∠CAE计算即可.
∠CAB=35°,∠AEC=90°,则∠CAE=90°-∠C=30°,然后利用∠DAE=∠CAD-∠CAE计算即可.
(2)根据题意可以用∠B和∠C表示出∠CAD和∠CAE,从而可以得到∠DAE与∠C-∠B的关系.
(1)在△ABC中,∵∠B=50°,∠C=60°,
∴∠BAC=180°-50°-60°=70°.
∵AD是∠BAC的角平分线,
∴∠BAD=∠DAC=![]() ∠BAC=35°.
∠BAC=35°.
又∵AE是BC上的高,
∴∠AEC=90°.
在△CAE中,∠CAE=90°-∠C=90°-60°=30°,
∴∠DAE=∠CAD-∠CAE=35°-30°=5°.
(2)∠ DAE =![]() (∠C-∠B).
(∠C-∠B).
证明如下:
∵AE是△ABC的高,
∴∠AEC=90°,
∴∠EAC=90°-∠C,
∵AD是△ABC的角平分线,
∴∠DAC=![]() ∠BAC.
∠BAC.
∵∠BAC=180°-∠B-∠C,
∴∠DAC=![]() (180°-∠B-∠C) ,
(180°-∠B-∠C) ,
∴∠DAE=∠DAC-∠EAC
=![]() (180°-∠B-∠C) - (90°-∠C)
(180°-∠B-∠C) - (90°-∠C)
=![]() (∠C-∠B)
(∠C-∠B)


科目:初中数学 来源: 题型:
【题目】有一种“二十四点”的游戏,其游戏规则是这样的:任取四个1至13之间的自然数,将这四个数(每个数用且只能用一次)进行加减乘除四则运算,使其结果等于24.例如对1,2,3,4,可作如下运算:(1+2+3)×4=24(上述运算与4×(1+2+3)视为相同方法的运算)现有四个有理数3,4,-6,10,运用上述规则写出三种不同方法的运算式,可以使用括号,使其结果等于24.运算式如下:
(1)____________________________;
(2)____________________________;
(3)____________________________;
另有四个有理数3,-5,7,-13,可通过运算式
(4)____________________________使其结果等于24.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“读书破万卷,下笔如有神”,这是古人关于读书的成功经验.开展课外阅读可以引起学生浓厚的学习兴趣和探求知识的强烈欲望,丰富知识,开阔视野,也有利于学习和巩固老师在课堂上所教的基础知识,使学生学得有趣,学得扎实,学得活泼,是启发智慧和锻炼才能的一条重要途径.为了创设全新的校园文化氛围,进一步组织学生开展课外阅读,让学生在丰富多彩的书海中,扩大知识源,亲近母语,提高文学素养.某校准备开展“与经典为友、与名著为伴”的阅读活动,活动前对本校学生进行了“你最喜欢的图书类型(只写一项)”的随机抽样调查,相关数据统计如下:

请根据以上信息解答下列问题:
(1)该校对多少名学生进行了抽样调查?
(2)请将图1和图2补充完整,并求出扇形统计图中小说所对应的圆心角度数.
(3)已知该校共有学生800人,利用样本数据估计全校学生中最喜欢小说人数约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明租用共享单车从家出发,匀速骑行到相距2400米的邮局办事.小明出发的同时,他的爸爸以每分钟100米的速度从邮局沿同一条道路步行回家,小明在邮局停留了2分钟后沿原路按原速返回.设他们出发后经过t(分)时,小明与家之间的距离为s1(米),小明爸爸与家之间的距离为s2(米),图中折线OABD,线段EF分别表示s1,s2与t之间的函数关系的图象.
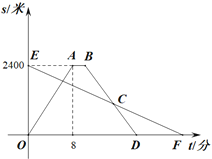
(1)求s1与t之间的函数表达式;
(2)小明从家出发,经过_______分在返回途中追上爸爸.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点P的坐标为(a,b),点P的“关联点”P’的坐标定义如下:当![]() 时,P’点坐标为(b,a);当
时,P’点坐标为(b,a);当![]() 时,P’点坐标为(-a,-b).
时,P’点坐标为(-a,-b).
(1)写出A(5,3)的变换点坐标_____,B(1,6)的变换点坐标______,C(-2,4)的变换点坐标_____;
(2)如果直线l:![]() 上所有点的关联点组成一个新的图形,记作图形W,请画出图形W;
上所有点的关联点组成一个新的图形,记作图形W,请画出图形W;
(3)在(2)的条件下,若直线y=kx-1(k≠0)与图形W有两个交点,请直接写出k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)请在横线上填写合适的内容,完成下面的证明:
如图①如果AB∥CD,求证:∠APC=∠A+∠C.
证明:过P作PM∥AB.
所以∠A=∠APM,( )
因为PM∥AB,AB∥CD(已知)
所以∠C= ( )
因为∠APC=∠APM+∠CPM
所以∠APC=∠A+∠C(等量代换)
(2)如图②,AB∥CD,根据上面的推理方法,直接写出∠A+∠P+∠Q+∠C= .
(3)如图③,AB∥CD,若∠ABP=x,∠BPQ=y,∠PQC=z,∠QCD=m,则m= (用x、y、z表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )

A. 函数有最小值
B. 对称轴是直线x=![]()
C. 当x<![]() ,y随x的增大而减小
,y随x的增大而减小
D. 当﹣1<x<2时,y>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在读书月活动中,学校准备购买一批课外读物,为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根据调查结果绘制的两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了多少名同学;
(2)条形统计图中,m,n的值;
(3)扇形统计图中,求出艺术类读物所在扇形的圆心角的度数;
(4)学校计划购买课外读物6000册,请根据样本数据,估计学校应购买其他类读物多少册?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com