
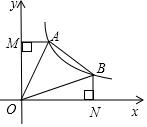
 如图,直线y=-x+b(b>0)与双曲线y=$\frac{k}{x}$(x>0)交于A、B两点,连接OA、OB,AM⊥y轴于M,BN⊥x轴于N,现有以下结论:
如图,直线y=-x+b(b>0)与双曲线y=$\frac{k}{x}$(x>0)交于A、B两点,连接OA、OB,AM⊥y轴于M,BN⊥x轴于N,现有以下结论:分析 ②设点A(x1,y1),B(x2,y2),根据反比例函数图象上点的坐标即可得出x1•y1=x2•y2=k,将y=-x+b代入y=$\frac{k}{x}$中,整理后根据根与系数的关系即可得出x1•x2=k,从而得出x2=y1、x1=y2,即ON=OM、AM=BN,利用全等三角形的判定定理SAS即可证出△AOM≌△BON,②正确;根据全等三角形的性质即可得出OA=OB,①正确;③作OH⊥AB于点H,根据等腰三角形的性质和全等三角形的性质即可得出∠AOH=∠BOH=22.5°、∠AOM=∠BON=22.5°,由相等的边角关系利用全等三角形的判定定理AAS即可证出△AOM≌△AOH,同理即可得出△AOM≌△AOH≌△BON≌△BOH,再利用反比例系数k的几何意义即可得出S△AOB=k,③正确;④延长MA、NB交于G点,由NG=OM=ON=MG、BN=AM可得出GB=GA,进而得出△ABG为等腰直角三角形,结合等腰直角三角形的性质以及AB=$\sqrt{2}$即可得出GA、GB的长度,由OM、ON的值不确定故无法得出AM、BN的值,④错误.综上即可得出结论.
解答 解:②设点A(x1,y1),B(x2,y2),
∵点A、B在双曲线y=$\frac{k}{x}$上,
∴x1•y1=x2•y2=k.
将y=-x+b代入y=$\frac{k}{x}$中,整理得:x2-bx+k=0,
∴x1•x2=k,
又∵x1•y1=k,
∴x2=y1,x1=y2,
∴ON=OM,AM=BN.
在△OMA和△ONB中,$\left\{\begin{array}{l}{OM=ON}\\{∠OMA=∠ONB}\\{AM=BN}\end{array}\right.$,
∴△AOM≌△BON(SAS),②正确;
①∵△AOM≌△BON,
∴OA=OB,
∴①OA=OB,②△AOM≌△BON,正确;
③作OH⊥AB于点H,如图1所示.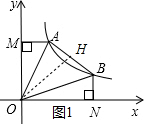
∵OA=OB,∠AOB=45°,△AOM≌△BON,
∴∠AOH=∠BOH=22.5°,∠AOM=∠BON=22.5°.
在△AOM和△AOH中,$\left\{\begin{array}{l}{∠OMA=∠OHA=90°}\\{∠AOM=∠AOH=22.5°}\\{OA=OA}\end{array}\right.$,
∴△AOM≌△AOH(AAS),
同理:△BON≌△BOH,
∴△AOM≌△AOH≌△BON≌△BOH,
∴S△AOB=S△AOH+S△BOH=S△AOM+S△BON=$\frac{1}{2}$k+$\frac{1}{2}$k=k,③正确;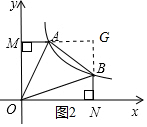
④延长MA、NB交于G点,如图2所示.
∵NG=OM=ON=MG,BN=AM,
∴GB=GA,
∴△ABG为等腰直角三角形,
当AB=$\sqrt{2}$时,GA=GB=$\frac{\sqrt{2}}{2}$AB=1,
∵OM、ON不确定,
∴无法得出AM=AN=1,④错误.
综上所述:结论正确的是①②③.
故答案为:①②③.
点评 本题考查了反比例函数与一次函数的交点问题、全等三角形的判定与性质、等腰直角三角形的判定与性质、反比例函数图象上点的坐标特征以及反比例系数k的几何意义,逐一分析四个结论的正误是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
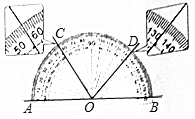 已知直线AB,射线OC,OD都在如图所示的量角器上,点O在直线AB上,则下列判断中不正确的是( )
已知直线AB,射线OC,OD都在如图所示的量角器上,点O在直线AB上,则下列判断中不正确的是( )| A. | ∠AOC=56° | B. | ∠AOD=134° | C. | ∠AOC<∠COD | D. | ∠BOD与∠BOC互补 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
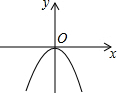 已知二次函数y=ax2的图象如图所示,则关于x的一元二次方程x2+x+a-1=0的根的存在情况是( )
已知二次函数y=ax2的图象如图所示,则关于x的一元二次方程x2+x+a-1=0的根的存在情况是( )| A. | 没有实数根 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com