
分析 分两种情况进行讨论:①在环形跑道上两人背向而行属于相遇问题,等量关系为:甲路程+乙路程=400;②两人同向而行相遇属于追击问题,等量关系为:甲路程-乙路程=400.
解答 解:设经过x秒后两人首次相遇.分两种情况:
①当两人同向而跑时,根据题意,得:
7x-5.5x=400,
解得:x=$\frac{800}{3}$;
②当两人相向而跑时,根据题意,得:
7x+5.5x=400,
解得:x=32.
答:经过32秒或$\frac{800}{3}$秒后两人首次相遇.
点评 本题考查了一元一次方程的应用中环形跑道上的相遇问题和追击问题.相遇问题常用的等量关系为:甲路程+乙路程=环形跑道的长度,追击问题常用的等量关系为:甲路程-乙路程=环形跑道的长度.


科目:初中数学 来源: 题型:解答题
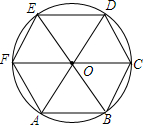 如图所示,△OAB为正三角形,以点O为圆心,OA为半径作⊙O,直径FC∥AB,AO,BO的延长线分别交⊙O于点D,E.
如图所示,△OAB为正三角形,以点O为圆心,OA为半径作⊙O,直径FC∥AB,AO,BO的延长线分别交⊙O于点D,E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
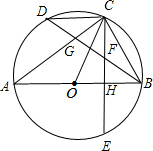 如图,AB是⊙O的直径,BD是弦,C是弧BD的中点,弦CE⊥AB,H是垂足,BD交CE,CA于点F,G.
如图,AB是⊙O的直径,BD是弦,C是弧BD的中点,弦CE⊥AB,H是垂足,BD交CE,CA于点F,G.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
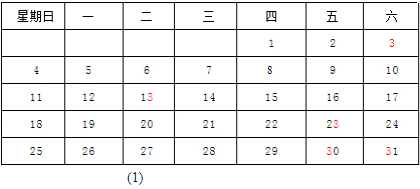
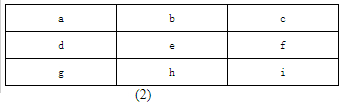
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com