
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
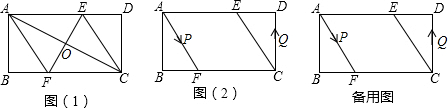
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
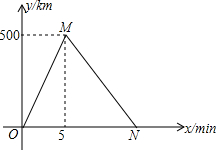 小亮和小华的家住在滨河大道旁,周六早上,他们两个相约去滨河大道上训练跑步,他们从A路口出发,沿滨河大道跑到B路口再原路返回,因为体力的原因,他们返回的平均速度都是各自出发时速度的$\frac{4}{5}$,设出发时间为x min,距A路口的距离为y cm,图中折线表示小亮在整个训练过程中y与x之间的函数关系图象.
小亮和小华的家住在滨河大道旁,周六早上,他们两个相约去滨河大道上训练跑步,他们从A路口出发,沿滨河大道跑到B路口再原路返回,因为体力的原因,他们返回的平均速度都是各自出发时速度的$\frac{4}{5}$,设出发时间为x min,距A路口的距离为y cm,图中折线表示小亮在整个训练过程中y与x之间的函数关系图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com