
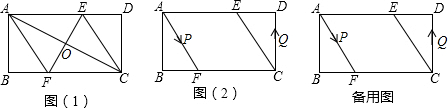
���� ��1��֤����AOE�ա�COF������֤��OA=OC��Ȼ����ݶԽ�������һ��ഹֱ���ı��������Σ�֤���ı���AFCE�����μ��ɵõ���AF��ȵ��߶Σ���ֱ�ǡ�ABF�����ù��ɶ����������AF�ij���
��2���ٷֳɵ�0��t��1��1��t��$\frac{8}{5}$��$\frac{8}{5}$��t��$\frac{7}{4}$��$\frac{7}{4}$��t��$\frac{12}{5}$��$\frac{12}{5}$��t��3��������������ۣ�ȷ��ÿ�������P��Q��λ�ã�������⣻
�ڸ��ݢٵĽ������ֱ����⣮
��� �⣺��1����ƽ���ı���ABCD�У�AD��BC��
���DAC=��ACF��
���ڡ�AOE�͡�COF�У�$\left\{\begin{array}{l}{��DAC=��ACF}\\{��AOE=��COF}\\{OE=OF}\end{array}\right.$��
���AOE�ա�COF��
��OA=OC��
�֡�OE=OF��AC��EF��
���ı���AFCE�����Σ�
��AF=FC=EC=AE��
��AF=x����BF=8-x��cm����
��ֱ�ǡ�ABF�У�AB2+BF2=AF2����42+��8-x��2=x2��
��ã�x=5��
�ʴ��ǣ�FC��EC��AE��5��
��2���ٵ�0��t��1ʱ��P��AF�ϣ�Q��CD�ϣ�AP��CQ��ƽ�У����ܹ���ƽ���ı��Σ�
��1��t��$\frac{8}{5}$ʱ��P��BF�ϣ�DE��AD�ϣ���5+5��t-1��=8-4��t-1����
��ã�t=$\frac{4}{3}$��
��$\frac{8}{5}$��t��$\frac{7}{4}$ʱ��P��AB�ϣ�Q��DE�ϣ����ܹ���ƽ���ı��Σ�
��$\frac{7}{4}$��t��$\frac{12}{5}$ʱ��P��AB�ϣ�Q��EC�ϣ�AP��EC��ƽ�У����ܹ���ƽ���ı��Σ�
��$\frac{12}{5}$��t��3ʱ��P��A�㣬���ܹ���ƽ���ı��Σ�
��֮��t=$\frac{4}{3}$���룩��
�ڵ�t=$\frac{4}{3}$ʱ��a=5��$\frac{4}{3}$=$\frac{20}{3}$��cm����
b=4��$\frac{4}{3}$=$\frac{16}{3}$��cm����
��a+b=$\frac{20}{3}$+$\frac{16}{3}$=12��cm����
�ʴ��ǣ�12cm��
���� ���⿼�������ε��ж��������Լ����ɶ�����Ӧ�ã���ȷ�������ۣ�ȷ��P��Q��λ���ǹؼ���


 ��Ԫ������ĩ��ϵ�д�
��Ԫ������ĩ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{\frac{1}{3}}$ | B�� | $\frac{1}{\sqrt{3}}$ | C�� | $\sqrt{\frac{2}{3}}$ | D�� | $\sqrt{12}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
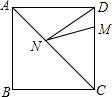 ��ͼ��������ABCD�ı߳�Ϊ8��M��DC�ϣ���DM=2��N��AC��һ���㣬��DN+MN����СֵΪ��������
��ͼ��������ABCD�ı߳�Ϊ8��M��DC�ϣ���DM=2��N��AC��һ���㣬��DN+MN����СֵΪ��������| A�� | 6 | B�� | 8 | C�� | 12 | D�� | 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
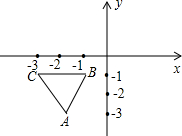 ��ƽ��ֱ������ϵ�У��涨��һ��������������x�ᷭ�ۣ�������ƽ��3����λ��Ϊ1�α任����ͼ����֪�ȱ�������ABC�Ķ���B��C������ֱ��ǣ�-1��-1������-3��-1�����ѡ�ABC��������8�������ı任�õ���A��B��C�䣬���A�Ķ�Ӧ��A��������ǣ�14��-1-$\sqrt{3}$����
��ƽ��ֱ������ϵ�У��涨��һ��������������x�ᷭ�ۣ�������ƽ��3����λ��Ϊ1�α任����ͼ����֪�ȱ�������ABC�Ķ���B��C������ֱ��ǣ�-1��-1������-3��-1�����ѡ�ABC��������8�������ı任�õ���A��B��C�䣬���A�Ķ�Ӧ��A��������ǣ�14��-1-$\sqrt{3}$�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
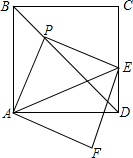 ��ͼ����PΪ������ABCD�ĶԽ���BD�ϵ�һ�����㣨����B��D�غϣ�������P��PE��AP������CD�ڵ�E������E��EF��PE��AP�Ĵ���AF�ڵ�F��
��ͼ����PΪ������ABCD�ĶԽ���BD�ϵ�һ�����㣨����B��D�غϣ�������P��PE��AP������CD�ڵ�E������E��EF��PE��AP�Ĵ���AF�ڵ�F���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com