练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
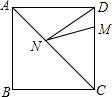
    12．如图，正方形ABCD的边长为8，M在DC上，且DM=2，N是AC上一动点，则DN+MN的最小值为（　　）
    A．6B．8C．12D．10

    分析 要求DN+MN的最小值，DN，MN不能直接求，可考虑通过作辅助线转化DN，MN的值，从而找出其最小值求解．

    解答 解：如图，连接BM，

    ∵点B和点D关于直线AC对称，
    ∴NB=ND，
    则BM就是DN+MN的最小值，
    ∵正方形ABCD的边长是8，DM=2，
    ∴CM=6，
    ∴BM=$\sqrt{{6}^{2}+{8}^{2}}$=10，
    ∴DN+MN的最小值是10．
    故选D．

    点评 此题考查正方形的性质和轴对称及勾股定理等知识的综合应用，解题的难点在于确定满足条件的点N的位置：利用轴对称的方法．然后熟练运用勾股定理．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    2．如图，在长方形ABCD中，已知AB=8cm，BC=10cm，将AD沿直线AF折叠，使点D落在BC的点E处，求CF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．现有4根小木棒，长度分别为：2、3、3、5（单位：cm），从中任意取出3根，请用画树状图法求它们能首尾顺次相接搭成三角形的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

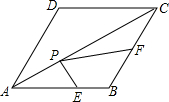    20．如图，在菱形ABCD中，AB=10，∠DAB=60°，P是对角线AC上一动点，E、F分别是线段AB和BC上的动点，则PE+PF的最小值是5$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．已知，矩形ABCD中，AB=4cm，BC=8cm，AC的垂直平分线EF分别交AD、BC于点E、F，垂足为O．连接AF、CE．
    （1）如图1，①写出所有和AF相等的线段．答：AE、CF、CE；②AF=5cm；
    （2）如图2，动点P、Q分别从A、C两点同时出发，沿△AFB和△CDE各边匀速运动一周．即点P自A→F→B→A停止，点Q自C→D→E→C停止．在运动过程中，
    ①已知点P的速度为每秒5cm，点Q的速度为每秒4cm，运动时间为t秒，当A、C、P、Q四点为顶点的四边形是平行四边形时，求t的值．
    ②若点P、Q的运动路程分别为a、b（单位：cm，ab≠0），已知A、C、P、Q四点为顶点的四边形是平行四边形，则a与b满足的数量关系是a+b=12cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．甲从M地出发去N地，乙搭甲的便车也从M地出发到途中与M，N两地在同一条直线上的G地．甲在N地停留一段时间后以110km/h的速度返回，乙在G地停留了$\frac{3}{4}$h后，徒步返回M地，走了5km时与返回的甲相遇并搭甲车返回M地．如图是两人与M地的距离y（单位：km）与行进时间x（单位：h）之间的函数图象（甲、乙均匀速行进，不考虑其他因素）．
    （1）求图象中线段FD的解析式；
    （2）甲在N地停留了几小时？
    （3）乙返回M地时，若一直徒步会比遇到甲搭甲的便车多用多长时间？请直接写出结果．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

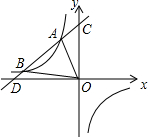    4．如图，A（-2，m）、B是双曲线y=-$\frac{8}{x}$上两点，直线AB：y=kx+b（k≠0，且k，b为常数）的图象经过点C（0，5），与x轴交于点D．
    （1）求直线AB的解析式和点B的坐标；
    （2）写出当x取何值时，关于x的不等式kx+b＜-$\frac{8}{x}$成立？
    （3）求S△AOB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．为了改善生态环境，某市计划将沟坡地退耕还林，结合实际，需种植A种用材林木和B种经济木两种，需要购买这两种树苗20万棵，设购买A种树苗x万棵，造这片树林的总费用为y元．已知y是x的一次函数，且当购买A种树苗3万棵时，总费用为242万元；购买A种树苗10万棵时，总费用为200万元．
    （1）写出y与x之间的函数关系式；
    （2）如果要求B种树苗的数量不超过A种树苗的3倍，问造这片树林至少要种多少A种树苗？并求出此时所需的总费用．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

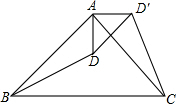    2．如图，△ABC是等腰直角三角形，BC是斜边，将△ABD绕点A逆时针旋转后，能与△ACD′重合．如果AD=2，那么DD′=2$\sqrt{2}$．

    查看答案和解析>>

    同步练习册答案