
分析 设甲水果的批发价为每千克x元,乙水果的批发价为每千克(x+0.5)元,根据100元买甲水果比150元买乙水果少10千克,列方程求解,然后判断是否赚钱.
解答 解:设甲水果的批发价为每千克x元,乙水果的批发价为每千克(x+0.5)元,
由题意得,$\frac{150}{x+0.5}$-$\frac{100}{x}$=10,
整理得:2x2-9x+10=0,
解得:x=2.5或x=2,
经检验,x=2.5或x=2都是原方程的根,但当x=2.5时,乙种水果批发价为3元,高于零售价,不合题意,舍去,
∴x=2.
∴甲种水果赚钱2.8×$\frac{100}{x}$($\frac{4}{5}$+$\frac{1}{5}$×$\frac{1}{2}$)-100=26(元);
乙种水果赚钱$\frac{150}{x+0.5}$×2.8-150=60×2.8-150=18(元);
两种水果总共赚钱26+18=44(元).
答:小明的爸爸共赚钱44元.
点评 本题考查了分式方程的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程求解,注意检验.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | y=0.12x,x>0 | B. | y=60-0.12x,x>0 | ||
| C. | y=0.12x,0≤x≤500 | D. | y=60-0.12x,0≤x≤500 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
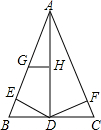 如图,已知AB=AC,AD是中线,BE=CF.
如图,已知AB=AC,AD是中线,BE=CF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
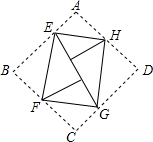 如图,有一个长(AB)为10cm的矩形纸板(即矩形ABCD),现将这个纸板的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH.若EF=8cm,则四边形EFGH的面积为( )
如图,有一个长(AB)为10cm的矩形纸板(即矩形ABCD),现将这个纸板的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH.若EF=8cm,则四边形EFGH的面积为( )| A. | 36cm2 | B. | 48cm2 | C. | 64cm2 | D. | 72cm2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com