
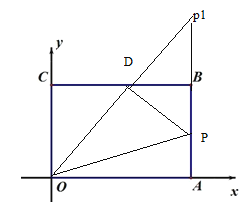
【题目】已知:如图,平面直角坐标系中,矩形OABC的顶点A(6,0)、B(6,4),D是BC的中点.动点P从O点出发,以每秒1个单位的速度,沿着OA、AB、BD运动.设P点运动的时间为t秒(0<t<13).

(1)写出△POD的面积S与t之间的函数关系式,并求出△POD的面积等于9时点P的坐标;
(2)当点P在OA上运动时,连结CP.问:是否存在某一时刻t,当CP绕点P旋转时,点C能恰好落到AB的中点M处?若存在,请求出t的值并判断此时△CPM的形状;若不存在,请说明理由;
(3)当点P在AB上运动时,试探索当PO+PD的长最短时的直线PD的表达式。
【答案】(1)(4.5,0)(2,4)(2)存在(3)y=-![]()
【解析】
试题分析:(1)根据矩形的性质得OA=BC=6,CD=BD=3,AB=4,然后分三种情况求解:当0<t≤6,如图1,OP=t,根据三角形面积公式得S=2t,再求出S=9所对应的t的值,然后写出此时P点坐标;当6<t≤10,如图2,则AP=t-6,BP=10-t,利用S=S矩形ABCD-S△OCD-S△OAP-S△BPD得到S=-![]() t+21,再求出S=9所对应的t的值,然后写出此时P点坐标;当10<t<13,如图3,则PB=13-t,根据三角形的面积公式得S=-2t+26,由于S=9时,计算出t=7.5,而7.5不合题意故舍去;
t+21,再求出S=9所对应的t的值,然后写出此时P点坐标;当10<t<13,如图3,则PB=13-t,根据三角形的面积公式得S=-2t+26,由于S=9时,计算出t=7.5,而7.5不合题意故舍去;
(2)如图4,E点为AB的中点,根据旋转的性质得PC=PE,在Rt△POC中,利用勾股定理得PC2=t2+42;在Rt△PAE中,利用勾股定理得到PE2=(6-t)2+22,则t2+42=(6-t)2+22,解方程得t=2.
(3)根据对称性找到P点的对称点P1,找到D点,然后求出D点的坐标,再根据待定系数法求出解析式.
试题解析:(1)∵矩形OABC的顶点A(6,0)、B(6,4),D是BC的中点,
∴OA=BC=6,CD=BD=3,AB=4,
当点P在OA上运动时,即0<t≤6,如图1,OP=t,S=![]() t4=2t;
t4=2t;
∵S=9,
∴2t=9,解得t=4.5,
∴此时P点坐标为(4.5,0);
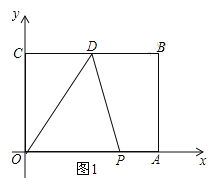
当点P在AB上运动时,即6<t≤10,如图2,AP=t-6,BP=10-t,S=S矩形ABCD-S△OCD-S△OAP-S△BPD
=4×6-![]() 4×3-
4×3-![]() 6(t-6)-
6(t-6)-![]() 3(10-t)
3(10-t)
=-![]() t+21;
t+21;
∵S=9,
∴-![]() t+21=9,解得t=8,
t+21=9,解得t=8,
∴此时P点坐标为(2,4);
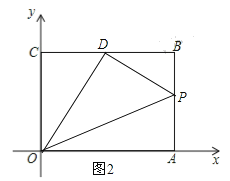
当点P在BD上运动时,即10<t<13,如图3,PB=13-t,S=![]() (13-t)4=-2t+26;
(13-t)4=-2t+26;
∵S=9,
∴-2t+26=9,解得t=7.5(不合题意舍去);
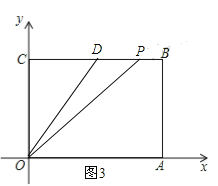
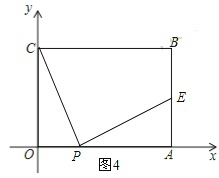
(2)存在.
如图4,E点为AB的中点,
∵CP绕点P旋转时,点C能恰好落到AB的中点,
∴PC=PE,
在Rt△POC中,OC=4,OP=t,
∴PC2=OP2+OC2=t2+42,
在Rt△PAE中,AE=2,PA=6-t,
∴PE2=PA2+AE2=(6-t)2+22,
∴t2+42=(6-t)2+22,解得t=2,
即当t=2s时,当CP绕点P旋转时,点C能恰好落到AB的中点处.
(3)y=-


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
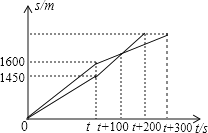
【题目】在一次越野赛跑中,当小明跑了1600m时,小刚跑了1450m,此后两人分别调整速度,并以各自新的速度匀速跑,又过100s时小刚追上小明,200s时小刚到达终点,300s时小明到达终点.他们赛跑使用时间t(s)及所跑距离如图s(m),这次越野赛的赛跑全程为 m?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嫦娥四号探测器于2019年1月3日,成功着陆在月球背面,通过“鹊桥”中继星传回了世界第一张近距离拍摄的月背影像图,开启了人类月球探测新篇章.当中继星成功运行于地月拉格朗日L2点时,它距离地球约1500000km.用科学记数法表示数1500000为( )

A. 15×105 B. 1.5×106 C. 0.15×107 D. 1.5×105
查看答案和解析>>
科目:初中数学 来源: 题型:
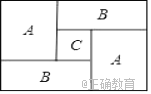
【题目】如图,一个长方形运动场被分隔成![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 共
共![]() 个区,
个区, ![]() 区是边长为
区是边长为![]() 的正方形,
的正方形, ![]() 区是边长为
区是边长为![]() 的正方形.
的正方形.
(1)列式表示每个![]() 区长方形场地的周长,并将式子化简;
区长方形场地的周长,并将式子化简;
(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)如果![]() ,
, ![]() ,求整个长方形运动场的面积.
,求整个长方形运动场的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,某校政教处对部分学生及家长就校园安全知识的了解程度进行了随机抽样调查,并绘制成如图所示的两幅统计图,请根据统计图中的信息,解答下列问题:
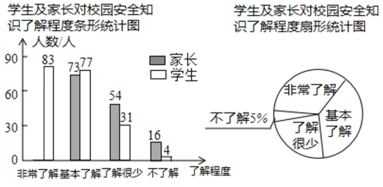
![]() 参与调查的学生及家长共有 人;
参与调查的学生及家长共有 人;
![]() 在扇形统计图中,求“基本了解"所对应的扇形的圆心角的度数;
在扇形统计图中,求“基本了解"所对应的扇形的圆心角的度数;
![]() 在条形统计图中,“非常了解”所对应的学生人数是______人 并补全条形统计图.
在条形统计图中,“非常了解”所对应的学生人数是______人 并补全条形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强学生的身体素质,某校长年坚持全员体育锻炼,并定期进行体能测试,下图是将某班学生的立定跳远成绩(精确到0.01米)进行整理后,画出的频数分布直方图的一部分,已知从左到右4个小组的频率分别是0.05,0.15,0.30,0.35,第5小组的频数9.
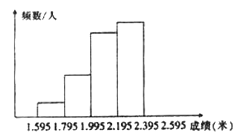
(1)请将频数分布直方图补充完整;
(2)该班参加这次测试的学生有多少人?
(3)若成绩在2.00米以上(含2.00米)的为合格,问该班成绩的合格率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两城相距900千米,一辆客车从A城开往B城,车速为每小时80千米,同时一辆出租车从B城开往A城,车速为每小时100千米,设客车出发时间为t(小时).
探究 若客车、出租车距A城的距离分别为y1、y2,写出y1、y2关于t的函数关系式及自变量取值范围,并计算当y1=240千米时y2的値.
发现 (1)设点C是A城与B城的中点,AC=![]() AB,通过计算说明:哪个车先到达C城?该车到达C后再经过多少小时,另一个车会到达C?
AB,通过计算说明:哪个车先到达C城?该车到达C后再经过多少小时,另一个车会到达C?
(2)若两车扣相距100千米时,求时间t.
决策 已知客车和出租车正好在A,B之间的服务站D处相遇,此时出租车乘客小王突然接到开会通知,需要立即返回,此时小王有两种选择返回B城的方案:
方案一:继续乘坐出租车到C城,加油后立刻返回B城,出租车加油时间忽略不计;
方案二:在D处换乘客车返回B城.
试通过计算,分析小王选择哪种方式能更快到达B城?
查看答案和解析>>
科目:初中数学 来源: 题型:
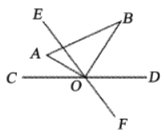
【题目】如图,直线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,将一直角三角尺
,将一直角三角尺![]() 的直角顶点与点
的直角顶点与点![]() 重合,
重合,![]() 平分
平分![]() .
.
(1)![]() 的度数为______________
的度数为______________![]() ;
;
(2)将三角尺![]() 以每秒
以每秒![]() 的速度绕点
的速度绕点![]() 顺时针旋转,同时直线
顺时针旋转,同时直线![]() 也以每秒
也以每秒![]() 的速度绕点
的速度绕点![]() 顺时针旋转,设运动时间为
顺时针旋转,设运动时间为![]() 秒
秒![]() .
.
①求当![]() 为何值时,直线
为何值时,直线![]() 平分
平分![]() ;
;
②求当![]() 为何值时,直线
为何值时,直线![]() 平分
平分![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com