【题目】如图，⊙O是Rt△ABC的外接圆，∠ACB=90°，∠A=25°，过点C作圆O的切线，交AB的延长线于点D，则∠D的度数是 ．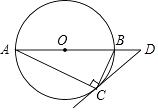 
【答案】40°
【解析】解：连接OC，如图所示．
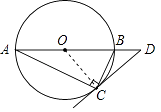
∵OA=OC，∠A=25°，
∴∠OCA=∠A=25°．
∵CD为⊙O的切线，
∴∠OCD=90°，
∴∠ACD=∠ACO+∠OCD=25°+90°=115°，
∴∠D=180°﹣∠A﹣∠ACD=180°﹣25°﹣115°=40°．
所以答案是：40°．
【考点精析】本题主要考查了三角形的内角和外角和等腰三角形的性质的相关知识点，需要掌握三角形的三个内角中，只可能有一个内角是直角或钝角；直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角；等腰三角形的两个底角相等（简称：等边对等角）才能正确解答此题．
应用题作业本系列答案科目：初中数学 来源： 题型：
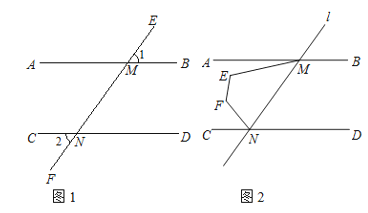
【题目】如图，直线l分别交AB,CD于点M,N(点M在点N的右侧)，若∠1=∠2
(1)求证:AB//CD；
(2)如图，点E、F在AB，CD之间，且在MN的左侧，若∠MEF+∠EFN=255°，求∠AME+∠FNC的度数；
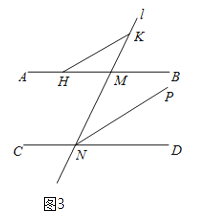
(3)如图,点H在直线AB上,且位于点M的左侧;点K在直线MN上,且在直线AB的上方.点Q在∠MND的角平分线NP上，且∠KHM=2∠MHQ，若∠HQN+∠HKN=75°，直接写出∠PND和∠QHB的数量关系.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：
中，
，
，点
为
内一点，连接
，
，
，过点
作
，交的延长线于点
.
（1）如图1，求证：
；
（2）如图2，点
为
的中点，分别连接
，
，求
的度数；
（3）如图3，在（2）的条件下，点
为
上一点，连接
，点
为的中点，连接
，过点作
，交的延长线于点
，若
，
的面积为30，
，求线段的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
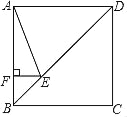
【题目】如图，正方形ABCD的边长为4，点E在对角线BD上，且∠DAE＝67.5°，EF⊥AB，垂足为F，则EF的长为（ ）
A. 1B. 
C. 4-2D. 3-4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们知道对于一个图形，通过不同的方法计算图形的面积可以得到一个数学等式．
例如：由图1可得到(a+b)=a+2ab+b．
图1 图2 图3
（1）写出由图2所表示的数学等式：_____________________；写出由图3所表示的数学等式：_____________________；
（2）利用上述结论，解决下面问题：已知a+b+c=11，bc+ac+ab=38，求a+b+c的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
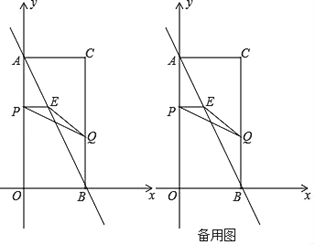
【题目】如图，在平面直角坐标系中，已知矩形AOBC的顶点C的坐标是（2，4），动点P从点A出发，沿线段AO向终点O运动，同时动点Q从点B出发，沿线段BC向终点C运动．点P、Q的运动速度均为每秒1个单位，设运动时间为t秒，过点P作PE⊥AO交AB于点E．
（1）求直线AB的解析式；
（2）在动点P、Q运动的过程中，以B、Q、E为顶点的三角形是直角三角形，直按写出t的值；
（3）设△PEQ的面积为S，求S与时间t的函数关系，并指出自变量t的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AD，BE分别是∠BAC，∠ABC的角平分线．
（1）若∠C＝70°，∠BAC＝60°，则∠BED的度数是 ；若∠BED＝50°，则∠C的度数是 ．
（2）探究∠BED与∠C的数量关系，并证明你的结论．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读理解：
小聪在解方程组
时，发现方程组中①和②之间存在一定的关系，他发现了一种“整体代换”法，具体解法如下：
解：将方程②变形为：
即
把方程①代入方程③得：
解得
把代入方程①得
∴方程组的解是
（1）模仿小聪的解法，解方程组
（2）已知x，y满足方程组
，解答：
（ⅰ）求
的值；
（ⅱ）求
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com