Question

【题目】已知：中，，，点为内一点，连接，，，过点作，交的延长线于点.

（1）如图1，求证：；

（2）如图2，点为的中点，分别连接，，求的度数；

（3）如图3，在（2）的条件下，点为上一点，连接，点为的中点，连接，过点作，交的延长线于点，若，的面积为30，，求线段的长.

Answer 1

【答案】(1)见解析;（2）45°;(3)10

【解析】

（1）根据全等三角形的判定得出△CAE≌△ABD，进而利用全等三角形的性质得出AE=BD；
（2）根据全等三角形的判定得出△AEH≌△BDH，进而利用全等三角形的性质解答；
（3）过点M作MS⊥FH于点S，过点E作ER⊥FH，交HF的延长线于点R，过点E作ET∥BC，根据全等三角形判定和性质解答即可．

证明：（1）∵CE⊥AE，BD⊥AE，
∴∠AEC=∠ADB=90°，
∵∠BAC=90°，
∴∠ACE+CAE=∠CAE+∠BAD=90°，
∴∠ACE=∠BAD，
在△CAE与△ABD中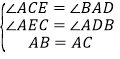

∴△CAE≌△ABD（AAS），
∴AE=BD；

（2）连接AH，如图2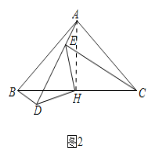

∵AB=AC，BH=CH，，
∴∠BAH=∠BAC＝×90°＝45°，∠AHB=90°，
∴∠ABH=∠BAH=45°，
∴AH=BH，
∵∠EAH=∠BAH-∠BAD=45°-∠BAD，
∠DBH=180°-∠ADB-∠BAD-∠ABH=45°-∠BAD，
∴∠EAH=∠DBH，
在△AEH与△BDH中
∴△AEH≌△BDH（SAS），
∴EH=DH，∠AHE=∠BHD，
∴∠AHE+∠EHB=∠BHD+∠EHB=90°
即∠EHD=90°，
∴∠EDH=∠DEH=＝45°
（3）过点M作MS⊥FH于点S，过点E作ER⊥FH，交HF的延长线于点R，过点E作ET∥BC，交HR的延长线于点T．如图3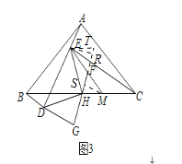

∵DG⊥FH，ER⊥FH，
∴∠DGH=∠ERH=90°，
∴∠HDG+∠DHG=90°
∵∠DHE=90°，
∴∠EHR+∠DHG=90°，
∴∠HDG=∠HER
在△DHG与△HER中

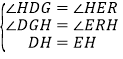∴△DHG≌△HER（AAS），
∴HG=ER，
∵ET∥BC，
∴∠ETF=∠BHG，∠EHB=∠HET，
∴∠ETF=∠FHM，
∵∠EHB=∠BHG，
∴∠HET=∠ETF，
∴HE=HT，
在△EFT与△MFH中

，
∴△EFT≌△MFH（AAS），
∴HF=FT，
∵＝，
∴ER=MS，
∴HG=ER=MS，
设GH=6k，FH=5k，则HG=ER=MS=6k，

∴＝＝30，
∴k=，
∴FH=5，
∴HE=HT=2HF=10，