
【题目】如图,已知![]() //
//![]() ,
,![]()
![]()
![]() ,∠
,∠![]() 和∠
和∠![]() 的角平分线交于点F,∠
的角平分线交于点F,∠![]() =__________°.
=__________°.
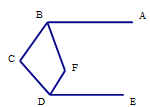
【答案】135;
【解析】
连接BD,根据三角形内角和定理得出∠C+∠CBD+∠CDB=180°,再由BC⊥CD可知∠C=90°,故∠CBD+∠CDB=90°,再由AB∥DE可知∠ABD+∠BDE=180°,故∠CBD+∠CDB+∠ABD+∠BDE =270°,再由∠ABC和∠CDE的平分线交于点F可得出∠CBF+∠CDF的度数,由四边形内角和定理即可得出结论.
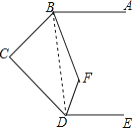
解:连接BD,
∵∠C+∠CBD+∠CDB=180°,BC⊥CD,
∴∠C=90°,
∴∠CBD+∠CDB=90°.
∵AB∥DE,
∴∠ABD+∠BDE=180°,
∴∠CBD+∠CDB+∠ABD+∠BDE=90°+180°=270°,即∠ABC+∠CDE=270°.
∵∠ABC和∠CDE的平分线交于点F,
∴∠CBF+∠CDF=![]() ×270°=135°,
×270°=135°,
∴∠BFD=360°-90°-135°=135°.
故答案为:135.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去,……,已知正方形ABCD的面积为S1为1,按上述方法所作的正方形的面积依次为S2,S3,……………,则Sn(n为正整数),那么第n个正方形的面积Sn等于( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l所对应的函数表达式为y=x.过点A1(0,1)作y轴的垂线交直线l于点B1 , 过点B1作直线l的垂线交y轴于点A2;过点A2作y轴的垂线交直线l于点B2 , 则点B2的坐标为( )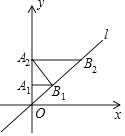
A.(1,1)
B.( ![]() ,
, ![]() )
)
C.(2,2)
D.( ![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校对初三学生进行物理、化学实验操作能力测试.物理、化学各有3个不同的操作实验题目,物理实验分别用①、②、③表示,化学实验分别用a、b、c表示.测试时每名学生每科只操作一个实验,实验的题目由学生抽签确定,第一次抽签确定物理实验题目,第二次抽签确定化学实验题目.王刚同学对物理的①、②号实验和化学的b、c号实验准备得较好.请用画树状图(或列表)的方法,求王刚同学同时抽到两科都准备得较好的实验题目的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一张边长为![]() 厘米的正方形桌面,因为实际需要,需将正方形边长增加
厘米的正方形桌面,因为实际需要,需将正方形边长增加![]() 厘米,木工师傅设计了如图所示的三种方案:
厘米,木工师傅设计了如图所示的三种方案:

小明发现这三种方案都能验证公式:![]() .
.
对于方案一,小明是这样验证的:
![]() 大正方形面积可表示为:
大正方形面积可表示为:![]() ,也可以表示为:
,也可以表示为:![]() ,
,
![]() .
.
请你仿照上述方法根据方案二、方案三,写出公式的验证过程.
(1)方案二:
(2)方案三:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 内一点,连接
内一点,连接![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.


(1)如图1,求证:![]() ;
;
(2)如图2,点![]() 为
为![]() 的中点,分别连接
的中点,分别连接![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(3)如图3,在(2)的条件下,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,点
,点![]() 为
为![]() 的中点,连接
的中点,连接![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,若
,若![]() ,
,![]() 的面积为30,
的面积为30,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 为第一象限内一点,点
为第一象限内一点,点![]() 为
为![]() 轴正半轴上一点,分别连接
轴正半轴上一点,分别连接![]() ,
,![]() ,
,![]() 为等边三角形,点
为等边三角形,点![]() 的横坐标为4.
的横坐标为4.

(1)如图1,求线段![]() 的长;
的长;
(2)如图2,点![]() 在线段
在线段![]() 上(点
上(点![]() 不与点
不与点![]() 、点
、点![]() 重合),点
重合),点![]() 在线段
在线段![]() 的延长线上,连接
的延长线上,连接![]() ,
,![]() ,
,![]() ,设
,设![]() 的长为
的长为![]() ,
,![]() 的长为
的长为![]() ,求
,求![]() 与
与![]() 的关系式(不要求写出
的关系式(不要求写出![]() 的取值范围)
的取值范围)
(3)在(2)的条件下,点![]() 为第四象限内一点,分别连接
为第四象限内一点,分别连接![]() ,
,![]() ,
,![]() ,
,![]() 为等边三角形,线段
为等边三角形,线段![]() 的垂直平分线交
的垂直平分线交![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,求点
,求点![]() 的横坐标.
的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道对于一个图形,通过不同的方法计算图形的面积可以得到一个数学等式.
例如:由图1可得到(a+b)=a+2ab+b.



图1 图2 图3
(1)写出由图2所表示的数学等式:_____________________;写出由图3所表示的数学等式:_____________________;
(2)利用上述结论,解决下面问题:已知a+b+c=11,bc+ac+ab=38,求a+b+c的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com