
【题目】在平面直角坐标系中,点![]() 为第一象限内一点,点
为第一象限内一点,点![]() 为
为![]() 轴正半轴上一点,分别连接
轴正半轴上一点,分别连接![]() ,
,![]() ,
,![]() 为等边三角形,点
为等边三角形,点![]() 的横坐标为4.
的横坐标为4.

(1)如图1,求线段![]() 的长;
的长;
(2)如图2,点![]() 在线段
在线段![]() 上(点
上(点![]() 不与点
不与点![]() 、点
、点![]() 重合),点
重合),点![]() 在线段
在线段![]() 的延长线上,连接
的延长线上,连接![]() ,
,![]() ,
,![]() ,设
,设![]() 的长为
的长为![]() ,
,![]() 的长为
的长为![]() ,求
,求![]() 与
与![]() 的关系式(不要求写出
的关系式(不要求写出![]() 的取值范围)
的取值范围)
(3)在(2)的条件下,点![]() 为第四象限内一点,分别连接
为第四象限内一点,分别连接![]() ,
,![]() ,
,![]() ,
,![]() 为等边三角形,线段
为等边三角形,线段![]() 的垂直平分线交
的垂直平分线交![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,求点
,求点![]() 的横坐标.
的横坐标.
【答案】(1)8;(2)d=t+8;(3)6
【解析】
(1)过点B作BH⊥OA于点H,根据等边三角形的性质解答即可;
(2)过点M作MP⊥AB于点P,根据等边三角形的性质解答即可;
(3)过点N作NK∥OB,交x轴于点K,过点N作NR⊥x轴于点R,通过等边三角形的性质和全等三角形的性质得到AN=8+t-8=t,OM=t,AH=MH=![]() AM=
AM=![]() (8-t)=4-
(8-t)=4-![]() t,
t,
OH=OM+MH=t+4-![]() t=4+
t=4+![]() t,通过证明AM=AN,可得关于t的方程,求出t,即可得点E的横坐标.
t,通过证明AM=AN,可得关于t的方程,求出t,即可得点E的横坐标.
解:(1)如图,过点B作BH⊥OA于点H,
∵△AOB为等边三角形,
∴BO=BA,
∵BH⊥OA,
∴OH=AH,
∵点B横坐标为4,
∴OH=4,
∴OA=2HO=8;
(2)如图,过点M作MP⊥AB于点P,
∴∠MPA=90°,
∵BM=MN,
∴BP=PN,
∵△AOB为等边三角形,
∴BA=AO=8,∠BAO=60°,
∴∠AMP=30°,
∴AP=![]() AM,
AM,
∵AM=8-t,
∴AP=![]() (8-t)=4-
(8-t)=4-![]() t,
t,
∴BP=AB-AP=4+![]() t,
t,
∴BN=2BP=8+t,
∴d=8+t
(3)过点N作NK∥OB,交x轴于点K,过点N作NR⊥x轴于点R,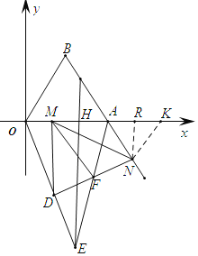
∵△AOB为等边三角形,
∴∠BOA=60°=∠OAB,
∵NK∥OB,
∴∠NKA=∠BOA=60°,且∠OAB=∠NAK=60°,
∴∠NAK=∠NKA=60°,
∴△AKN是等边三角形
∴AN=NK=AK,
∵△MND为等边三角形,
∴∠NMD=∠MND=60°,MN=MD,
∴∠OMD+∠NMK=∠NMK+∠MNK=180°-60°=120°,
∴∠OMD=∠MNK,
∵AN=8+t-8=t,OM=t,
∴OM=AN=NK=AK=t,且∠OMD=∠MNK,MD=MN,
∴△OMD≌△KNM(SAS),
∴OD=MK,∠MOD=∠MKN=60°,
∵MK=8-t+t=8,
∴OD=8,
∵EH垂直平分MA,
∴AH=MH=![]() AM=
AM=![]() (8-t)=4-
(8-t)=4-![]() t,
t,
∴OH=OM+MH=t+4-![]() t=4+
t=4+![]() t,
t,
∵∠OEH=90°-60°=30°,
∴OE=2HO=8+t,
∴DE=8+t-8=t,
∴DE=AN,
∵∠DOA=∠BAO,
∴BN∥OE,
∴∠NAF=∠DEF,
又∵∠AFN=∠EFD,AN=DE,
∴△AFN≌△EFD(AAS),
∴FN=FD,
又∵MN=MD,
∴MF⊥DN,
∵NR⊥AK,
∴∠ARN=90°,且∠NAK=60°,
∴∠ANR=30°,
∴AR=![]() AN,
AN,
∵MR=AM+AR=AM+![]() AN,MF=AM+
AN,MF=AM+![]() AN,
AN,
∴MR=MF,且MF⊥DN,NR⊥AK,
∴∠MNR=∠MND=60°,
∴∠NMA=90°-60°=30°,
∵∠BAO=∠AMN+∠ANM,
∴∠AMN=∠ANM=30°,
∴AM=AN,
∴8-t=t,
∴t=4,
∴OH=4+![]() ×4=6,
×4=6,
∴点E的横坐标为6.


科目:初中数学 来源: 题型:
【题目】为改善办学条件,北海中学计划购买部分![]() 品牌电脑和
品牌电脑和![]() 品牌课桌.第一次,用9万元购买了
品牌课桌.第一次,用9万元购买了![]() 品牌电脑10台和
品牌电脑10台和![]() 品牌课桌200张.第二次,用9万元购买了
品牌课桌200张.第二次,用9万元购买了![]() 品牌电脑12台和
品牌电脑12台和![]() 品牌课桌120张.
品牌课桌120张.
(1)每台![]() 品牌电脑与每张
品牌电脑与每张![]() 品牌课桌的价格各是多少元?
品牌课桌的价格各是多少元?
(2)第三次购买时,销售商对一次购买量大的客户打折销售.规定:一次购买![]() 品牌电脑35台以上(含35台),按九折销售,一次购买
品牌电脑35台以上(含35台),按九折销售,一次购买![]() 品牌课桌600张以上(含600张),按八折销售.学校准备用27万元购买电脑和课桌,其中电脑不少于35台,课桌不少于600张,问有几种购买方案?
品牌课桌600张以上(含600张),按八折销售.学校准备用27万元购买电脑和课桌,其中电脑不少于35台,课桌不少于600张,问有几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线 ![]() (a1>0)与抛物线
(a1>0)与抛物线 ![]() (a2<0)都经过y轴正半轴上的点A.过点A作x轴的平行线,分别与这两条抛物线交于B、C两点,以BC为边向下作等边△BCD,则△BCD的面积为 .
(a2<0)都经过y轴正半轴上的点A.过点A作x轴的平行线,分别与这两条抛物线交于B、C两点,以BC为边向下作等边△BCD,则△BCD的面积为 . 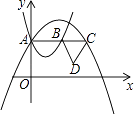
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD、EF被直线GH所截,已知AB//CD,∠1+∠2=180°,请填写CD//EF的理由.
解:因为∠1=∠3( )
_____________________(已知)
所以∠2+∠3=180°( )
得AB//EF( )
因为AB//CD( )
所以CD//EF( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于O点,且BE=BF,∠BEF=2∠BAC。

(1)求证:OE=OF;
(2)若BC=![]() ,求AB的长。
,求AB的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F,且AF=BD,连结BF.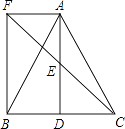
(1)求证:①△EAF≌△EDC;
②D是BC的中点;
(2)若AB=AC,求证:四边形AFBD是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是等边三角形,
是等边三角形,![]() .
.
![]() 如图1,点E为BC上一点,点F为AC上一点,且
如图1,点E为BC上一点,点F为AC上一点,且![]() ,连接AE,BF交于点G,求
,连接AE,BF交于点G,求![]() 的度数;
的度数;
![]() 如图2,点M是BC延长线上一点,
如图2,点M是BC延长线上一点,![]() ,MN交
,MN交![]() 的外角平分线于点N,求
的外角平分线于点N,求![]() 的值;
的值;
![]() 如图3,过点A作
如图3,过点A作![]() 于点D,点P是直线AD上一点,以CP为边,在CP的下方作等边
于点D,点P是直线AD上一点,以CP为边,在CP的下方作等边![]() ,连DQ,则DQ的最小值是______.
,连DQ,则DQ的最小值是______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com