
【题目】如图,在平面直角坐标系中,抛物线 ![]() (a1>0)与抛物线
(a1>0)与抛物线 ![]() (a2<0)都经过y轴正半轴上的点A.过点A作x轴的平行线,分别与这两条抛物线交于B、C两点,以BC为边向下作等边△BCD,则△BCD的面积为 .
(a2<0)都经过y轴正半轴上的点A.过点A作x轴的平行线,分别与这两条抛物线交于B、C两点,以BC为边向下作等边△BCD,则△BCD的面积为 . 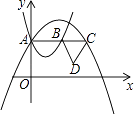
科目:初中数学 来源: 题型:
【题目】如图,AB//CD,点G在直线AB上, 点H在直线CD上,点K在AB、CD之间且在G、H所在直线的左侧, 若 ∠GKH=60°,点P为线段KH上一点(不和K、H重合),连接PG并延长到M, 设∠KHC=n∠KGP,要使得![]() 为定值,则n=_____
为定值,则n=_____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l所对应的函数表达式为y=x.过点A1(0,1)作y轴的垂线交直线l于点B1 , 过点B1作直线l的垂线交y轴于点A2;过点A2作y轴的垂线交直线l于点B2 , 则点B2的坐标为( )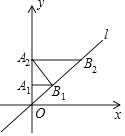
A.(1,1)
B.( ![]() ,
, ![]() )
)
C.(2,2)
D.( ![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
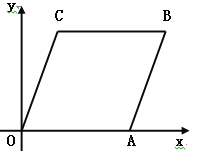
【题目】如图,在直角坐标系xoy中,已知A(6,0),B(8,6),将线段OA平移至CB,点D在x轴正半轴上(不与点A重合),连接OC,AB,CD,BD.
(1)写出点C的坐标;
(2)当△ODC的面积是△ABD的面积的3倍时,求点D的坐标;
(3)设∠OCD=α,∠DBA=β,∠BDC=θ,判断α、β、θ之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校对初三学生进行物理、化学实验操作能力测试.物理、化学各有3个不同的操作实验题目,物理实验分别用①、②、③表示,化学实验分别用a、b、c表示.测试时每名学生每科只操作一个实验,实验的题目由学生抽签确定,第一次抽签确定物理实验题目,第二次抽签确定化学实验题目.王刚同学对物理的①、②号实验和化学的b、c号实验准备得较好.请用画树状图(或列表)的方法,求王刚同学同时抽到两科都准备得较好的实验题目的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一张边长为![]() 厘米的正方形桌面,因为实际需要,需将正方形边长增加
厘米的正方形桌面,因为实际需要,需将正方形边长增加![]() 厘米,木工师傅设计了如图所示的三种方案:
厘米,木工师傅设计了如图所示的三种方案:

小明发现这三种方案都能验证公式:![]() .
.
对于方案一,小明是这样验证的:
![]() 大正方形面积可表示为:
大正方形面积可表示为:![]() ,也可以表示为:
,也可以表示为:![]() ,
,
![]() .
.
请你仿照上述方法根据方案二、方案三,写出公式的验证过程.
(1)方案二:
(2)方案三:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 为第一象限内一点,点
为第一象限内一点,点![]() 为
为![]() 轴正半轴上一点,分别连接
轴正半轴上一点,分别连接![]() ,
,![]() ,
,![]() 为等边三角形,点
为等边三角形,点![]() 的横坐标为4.
的横坐标为4.

(1)如图1,求线段![]() 的长;
的长;
(2)如图2,点![]() 在线段
在线段![]() 上(点
上(点![]() 不与点
不与点![]() 、点
、点![]() 重合),点
重合),点![]() 在线段
在线段![]() 的延长线上,连接
的延长线上,连接![]() ,
,![]() ,
,![]() ,设
,设![]() 的长为
的长为![]() ,
,![]() 的长为
的长为![]() ,求
,求![]() 与
与![]() 的关系式(不要求写出
的关系式(不要求写出![]() 的取值范围)
的取值范围)
(3)在(2)的条件下,点![]() 为第四象限内一点,分别连接
为第四象限内一点,分别连接![]() ,
,![]() ,
,![]() ,
,![]() 为等边三角形,线段
为等边三角形,线段![]() 的垂直平分线交
的垂直平分线交![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,求点
,求点![]() 的横坐标.
的横坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com