
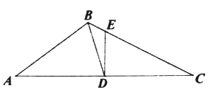
【题目】如图,![]() 中,
中,![]() 的垂直平分线
的垂直平分线![]() 分别交
分别交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() 的面积为54,则线段
的面积为54,则线段![]() 的长为__________.
的长为__________.
【答案】6![]()
【解析】
过C点作CN⊥AB的延长线于N,过B点作BM⊥AC于M,根据DE垂直平分AC,从而证出![]() ,再根据
,再根据![]() ,从而证出
,从而证出![]() ,证出MC=NC,设AB=x,DM=y,则CN=x+y,然后根据
,证出MC=NC,设AB=x,DM=y,则CN=x+y,然后根据![]() ,得到AB:AC=AM:AN,继而得出AN=2(x-y),在Rt
,得到AB:AC=AM:AN,继而得出AN=2(x-y),在Rt![]() 中,根据勾股定理得出x和y的关系,再根据
中,根据勾股定理得出x和y的关系,再根据![]() 的面积为54,所以有
的面积为54,所以有![]() 的面积也为54,所以
的面积也为54,所以![]() ,从而求出x、y的值,再根据BD2=x2-(x-y)2+y2,即可求出答案.
,从而求出x、y的值,再根据BD2=x2-(x-y)2+y2,即可求出答案.
过C点作CN⊥AB的延长线于N,过B点作BM⊥AC于M.

∵DE垂直平分AC
∴BM//DE
∴![]()
又∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∵BM⊥AC,CN⊥AB
∴MC=CN
设AB=x,DM=y
∵AB=AD, DE垂直平分AC
∴AD=CD=x,CN=x+y
∵![]() 的面积为54
的面积为54
∴![]() 的面积也为54
的面积也为54
∴![]()
∵![]() ,
,![]()
∴![]()
∴AB:AC=AM:AN=1: 2
∴AN=2AM=2(x-y)
在Rt![]() 中,根据勾股定理可得,(x+y)2+[2(x+y)]2=(2x)2
中,根据勾股定理可得,(x+y)2+[2(x+y)]2=(2x)2
解得,x=5y或x=y(不合题意舍去)
∵![]()
∴xy=36
在Rt![]() 中,BM2=x2—(x-y)2
中,BM2=x2—(x-y)2
在Rt![]() 中,BD2=x2-(x-y)2+y2=2xy
中,BD2=x2-(x-y)2+y2=2xy
∴BD2=72,
∴BD=6![]()
故答案为:6![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】一只不透明的箱子里共有3个球,其中2个白球,1个红球,它们除颜色外均相同.
(1)从箱子中随机摸出一个球是白球的概率是多少?
(2)从箱子中随机摸出一个球,记录下颜色后不将它放回箱子,搅匀后再摸出一个球,求两次摸出的球都是白球的概率,并画出树状图.
查看答案和解析>>
科目:初中数学 来源: 题型:
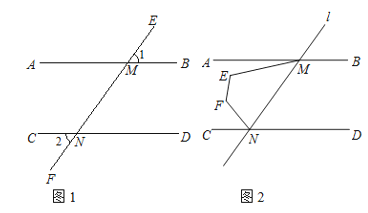
【题目】如图,直线l分别交AB,CD于点M,N(点M在点N的右侧),若∠1=∠2
(1)求证:AB//CD;
(2)如图,点E、F在AB,CD之间,且在MN的左侧,若∠MEF+∠EFN=255°,求∠AME+∠FNC的度数;
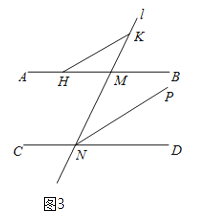
(3)如图,点H在直线AB上,且位于点M的左侧;点K在直线MN上,且在直线AB的上方.点Q在∠MND的角平分线NP上,且∠KHM=2∠MHQ,若∠HQN+∠HKN=75°,直接写出∠PND和∠QHB的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
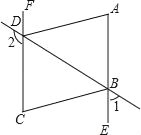
【题目】如图,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由;
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校对初三学生进行物理、化学实验操作能力测试.物理、化学各有3个不同的操作实验题目,物理实验分别用①、②、③表示,化学实验分别用a、b、c表示.测试时每名学生每科只操作一个实验,实验的题目由学生抽签确定,第一次抽签确定物理实验题目,第二次抽签确定化学实验题目.王刚同学对物理的①、②号实验和化学的b、c号实验准备得较好.请用画树状图(或列表)的方法,求王刚同学同时抽到两科都准备得较好的实验题目的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线![]() 、
、![]() 之间有一个直角三角形
之间有一个直角三角形![]() ,其中
,其中![]() ,
,![]() .
.
(1)如图,点![]() 在直线
在直线![]() 上,
上,![]() 、
、![]() 在直线
在直线![]() 上,若
上,若![]() ,
,![]() .试说明:
.试说明:![]() ;
;
(2)将三角形![]() 如图放置,直线
如图放置,直线![]() ,点
,点![]() 、
、![]() 分别在直线
分别在直线![]() 、
、![]() 上,且
上,且![]() 平分
平分![]() .求
.求![]() 的度数;(用
的度数;(用![]() 的代数式表示)
的代数式表示)
(3)在(2)的前提下,直线![]() 平分
平分![]() 交直线
交直线![]() 于
于![]() ,如图.在
,如图.在![]() 取不同数值时,
取不同数值时,![]() 的大小是否发生变化?若不变求其值,若变化请求出变化的范围.
的大小是否发生变化?若不变求其值,若变化请求出变化的范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 内一点,连接
内一点,连接![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.


(1)如图1,求证:![]() ;
;
(2)如图2,点![]() 为
为![]() 的中点,分别连接
的中点,分别连接![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(3)如图3,在(2)的条件下,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,点
,点![]() 为
为![]() 的中点,连接
的中点,连接![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,若
,若![]() ,
,![]() 的面积为30,
的面积为30,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
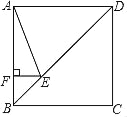
【题目】如图,正方形ABCD的边长为4,点E在对角线BD上,且∠DAE=67.5°,EF⊥AB,垂足为F,则EF的长为( )
A. 1B. ![]() C. 4-2
C. 4-2![]() D. 3
D. 3![]() -4
-4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
小聪在解方程组![]() 时,发现方程组中①和②之间存在一定的关系,他发现了一种“整体代换”法,具体解法如下:
时,发现方程组中①和②之间存在一定的关系,他发现了一种“整体代换”法,具体解法如下:
解:将方程②变形为:![]()
即![]()
把方程①代入方程③得:![]() 解得
解得![]()
把![]() 代入方程①得
代入方程①得![]()
∴方程组的解是![]()
(1)模仿小聪的解法,解方程组![]()
(2)已知x,y满足方程组![]() ,解答:
,解答:
(ⅰ)求![]() 的值;
的值;
(ⅱ)求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com