
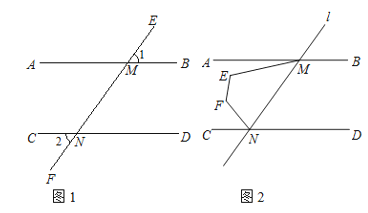
【题目】如图,直线l分别交AB,CD于点M,N(点M在点N的右侧),若∠1=∠2
(1)求证:AB//CD;
(2)如图,点E、F在AB,CD之间,且在MN的左侧,若∠MEF+∠EFN=255°,求∠AME+∠FNC的度数;
(3)如图,点H在直线AB上,且位于点M的左侧;点K在直线MN上,且在直线AB的上方.点Q在∠MND的角平分线NP上,且∠KHM=2∠MHQ,若∠HQN+∠HKN=75°,直接写出∠PND和∠QHB的数量关系.
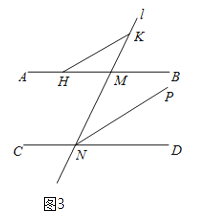
【答案】(1)见解析;(2)∠AME+∠FNC=75°;(3)∠PND-∠QHB=25°或3∠PND-∠QHB=75°
【解析】
(1)根据平行线的判定证出∠2=∠AMF即可;
(2)如图,过E,F分别作EH∥AB,FK∥AB,可得AB∥EH∥FK∥CD,根据平行线的性质即可求解;
(3)分两种情况考虑:HQ在∠KHM内和在∠KHM外,根据平行线的性质和三角形外角的性质分别求出结论即可.
(1)证明:∠1=∠AMF
又∠1=∠2
∴∠2=∠AMF
∴AB∥CD
(2)如图,过E,F分别作EH∥AB,FK∥AB
又AB∥CD ∴AB∥EH∥FK∥CD
∴∠HEF+∠EFK=180°
又∠MEF+∠EFN=255°
∴∠MEH+∠KFN=75°,
∵AB∥EH
∴∠MEH=∠AME,
∵ FK∥CD
∴∠FNC=∠KFN
∴∠AME+∠FNC=75°;

(3)∠PND-∠QHB=25° 或3∠PND-∠QHB=75°
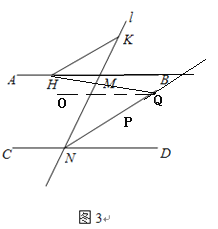
过Q作QO∥AB,则QO∥AB∥CD
∴∠KMB=∠MND=2∠PND,∠OQN=∠PND,∠OQH=∠MHQ
∴∠HQN=∠PND+∠MHQ
∠HKN=∠KMB-∠KHM=2∠PND-2∠MHQ
∵∠HQN+∠HKN=75°,
∴2∠PND-2∠MHQ+∠PND+∠MHQ=75°,即3∠PND-∠QHB=75°;
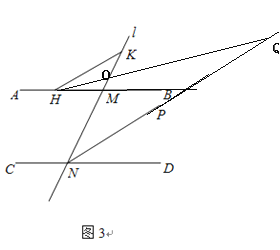
如图,∠HKN=∠KMB-∠KHM=2∠PND-2∠MHQ
∠HOM=∠OMB-∠MHQ=2∠PND-∠MHQ
∠HQN=∠HOM-∠MNB=∠HOM-∠PND=2∠PND-∠MHQ-∠PND=∠PND-∠MHQ
∵∠HQN+∠HKN=75°,
∴∠PND-∠MHQ+2∠PND-2∠MHQ=75°,即∠PND-∠QHB=25°.
故答案为:(1)见解析;(2)∠AME+∠FNC=75°;(3)∠PND-∠QHB=25°或3∠PND-∠QHB=75°.


科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E、F分别是边BC、AB上的点,且CE=BF,连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.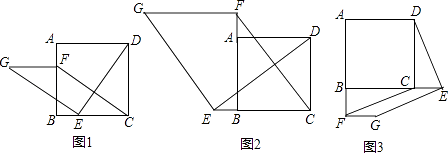
(1)请判断:FG与CE的数量关系和位置关系;(不要求证明)
(2)如图2,若点E、F分别是CB、BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请出判断判断予以证明;
(3)如图3,若点E、F分别是BC、AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,点P在AD上,AB=2,AP=1.将直角尺的顶点放在P处,直角尺的两边分别交AB,BC于点E,F,连接EF(如图①).
(1)当点E与点B重合时,点F恰好与点C重合(如图②),求PC的长;
(2)探究:将直尺从图②中的位置开始,绕点P顺时针旋转,当点E和点A重合时停止.在这个过程中,请你观察、猜想,并解答:
①tan∠PEF的值是否发生变化?请说明理由;
②直接写出从开始到停止,线段EF的中点经过的路线长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的顶点A、B的坐标分别是A(﹣1,0),B(0,﹣2),顶点C、D在双曲线y= ![]() 上,边AD交y轴于点E,且四边形BCDE的面积是△ABE面积的5倍,则k= .
上,边AD交y轴于点E,且四边形BCDE的面积是△ABE面积的5倍,则k= . 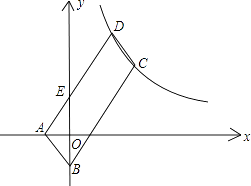
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在两条垂直相交的道路上,一辆自行车和一辆摩托车相遇后又分别向北向东驶去,若自行车与摩托车每秒分别行驶![]() 米、
米、![]() 米,则
米,则![]() 秒后两车相距( )米.
秒后两车相距( )米.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是⊙O的内接四边形,AB为⊙O的直径,连结BD.若∠BCD=120°,则∠ABD的大小为( )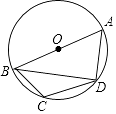
A.60°
B.50°
C.40°
D.30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,从点![]()
![]()
![]()
![]()
![]()
![]() ... 依次扩展下去,则
... 依次扩展下去,则 ![]() 的坐标为 ( )
的坐标为 ( )

A. (505,-505)B. (-505,505)C. (-505,504)D. (-506,505)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com