
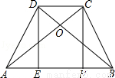
如图,梯形ABCD中,AB∥CD,AC⊥BD于点0,∠CDB=∠CAB,DE⊥AB,CF⊥AB,E.F为垂足.设DC=m,AB=n.(1)求证:△ACB≌△BDA;(2)求四边形DEFC的周长.
(1)证明见解析;(2)3m+n.
【解析】
试题分析:(1)根据已知和平行线的性质得出∠CDB=∠CAB=∠ABD=∠DCA,推出OA=OB,OC=OD,求出AC=BD,根据SAS证三角形全等即可;
(2)过点C作CG∥BD,交AB延长线于G,得出平行四边形DCGB,推出等腰直角三角形ACG,求出AG长,求出CF即可.
试题解析:(1)证明:∵AB∥CD,∠CDB=∠CAB,
∴∠CDB=∠CAB=∠ABD=∠DCA,
∴OA=OB,OC=OD,
∴AC=BD,
在△ACB与△BDA中,
 ,
,
∴△ACB≌△BDA.
(2)【解析】
过点C作CG∥BD,交AB延长线于G,
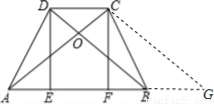
∵DC∥AG.CG∥BD,
∴四边形DBGC为平行四边形,
∵△ACB≌△BDA,
∴AD=BC,
即梯形ABCD为等腰梯形,
∵AC=BD=CG,
∴AC⊥BD,即AC⊥CG,又CF⊥AG,
∴∠ACG=90°,AC=BD,CF⊥FG,
∴AF=FG,
∴CF=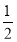 AG,又AG=AB+BG=m+n,
AG,又AG=AB+BG=m+n,
∴CF=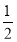 (m+n).
(m+n).
又∵四边形DEFC为矩形,故其周长为:2(DC+CF)=2(m+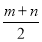 )=3m+n
)=3m+n
考点: 1.等腰梯形的判定;2.全等三角形的判定与性质;3.平行四边形的判定与性质;4.等腰梯形的性质.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源:2014中考名师推荐数学一元二次方程(解析版) 题型:解答题
某汽车销售公司6月份销售某厂家的汽车,在一定范围内,每部汽车的进价与销售量有如下关系:若当月仅售出1部汽车,则该部汽车的进价为27万元,每多售出1部,所有售出的汽车的进价均降低0.1万元/部,月底厂家根据销售量一次性返利给销售公司,销售量在10部以内(含10部),每部返利0.5万元;销售量在10部以上,每部返利1万元.
(1)若该公司当月售出3部汽车,则每部汽车的进价为 万元;
(2)如果汽车的售价为28万元/部,该公司计划当月盈利12万元,那么需要售出多少部汽车?(盈利=销售利润+返利)
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学一元一次不等式(解析版) 题型:选择题
设“、”“●”、“■”分别表示三种不同的物体,现用天平秤两次,情况如图所示,那么、●、■这三种物体按质量从大到小排列应为( )
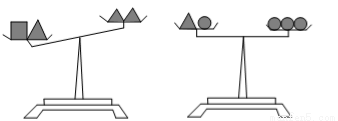
A.■、●、
B.、■、●
C.■、、●
D.●、、■
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学一元一次不等式组(解析版) 题型:选择题
对于实数x,我们规定[x]表示不大于x的最大整数,例如[1.2]=1,[3]=3,
[﹣2.5]=﹣3,若[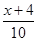 ]=5,则x的取值可以是( )
]=5,则x的取值可以是( )
A.40
B.45
C.51
D.56
查看答案和解析>>
科目:初中数学 来源:2013-2014学年黑龙江省大庆市九年级下学期期末数学试卷(解析版) 题型:填空题
一个口袋中装有10个红球和若干个黄球.在不允许将球倒出来数的前提下,为估计口袋中黄球的个数,小明采用了如下的方法:每次先从口袋中摸出10个球,求出其中红球数与10的比值,再把球放回口袋中摇匀.不断重复上述过程20次,得到红球数与10的比值的平均数为0.4.根据上述数据,估计口袋中大约有 _________ 个黄球.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年黑龙江省大庆市九年级下学期期末数学试卷(解析版) 题型:选择题
矩形的面积一定,则它的长和宽的关系是( )
A.正比例函数 B.一次函数 C.反比例函数 D.二次函数
查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市万州区岩口复兴学校九年级下学期期中命题(一)数学试卷(解析版) 题型:填空题
在平面直角坐标系中横、纵坐标均是整数的点称为整点,例如点(-1,4)是一个整点.直线y=-x+4与两坐标轴围成△AOB,点P是△AOB的边及其内部的整点,则点P落在以O为圆心,3为半径的圆内的概率为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com