
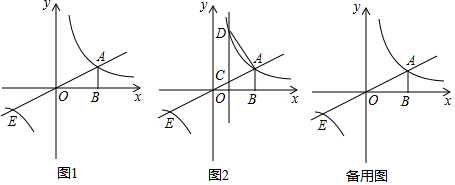
分析 (1)把A点坐标分别代入两个函数可求得结论;
(2)根据图象直接得出不等式k1x>$\frac{{k}_{2}}{x}$的解集;
(3)①如图2,表示出CD=$\frac{2}{x}-\frac{1}{2}x$,PB=2-x,代入面积公式可求得S与x的函数关系式,并根据OB=2,写出x的取值;
②分三种情况:
i)当AB为对角线时,此时CQ与AB互相垂直平分,
根据中点坐标公式得:C(1,$\frac{1}{2}$),Q(3,$\frac{1}{2}$);
ii)当AC为对角线时,此时过B作AC的垂线与AC交于点F,易得△ABF∽△AOB,由相似比可求得AF=$\frac{\sqrt{5}}{5}$,AC=$\frac{2\sqrt{5}}{5}$,由两点之间的距离可求得C($\frac{6}{5}$,$\frac{3}{5}$),Q($\frac{6}{5}$,$\frac{8}{5}$);
iii)当BC为对角线时,则AC=1,由两点的距离公式可求得C有两个值,根据横坐标不变,纵坐标减1可得此时对应的Q的坐标.
解答 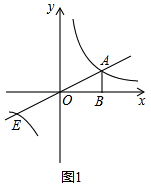 解:(1)把A(2,1)代入y=k1x中得:
解:(1)把A(2,1)代入y=k1x中得:
2k1=1,
k1=$\frac{1}{2}$,
∴直线的表达式为:y=$\frac{1}{2}$x;
把A(2,1)代入y=$\frac{{k}_{2}}{x}$中得:
1=$\frac{{k}_{2}}{2}$,k2=2,
∴双曲线的表达式为:y=$\frac{2}{x}$;
(2)如图1,∵点A(2,1),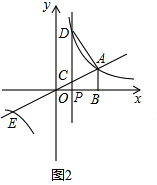
∴E(-2,-1),
由图象得不等式k1x>$\frac{{k}_{2}}{x}$的解集:-2<x<0或x>2,
故答案为:-2<x<0或x>2;
(3)①如图2,∵P(x,0),
∴D(x,$\frac{2}{x}$),C(x,$\frac{1}{2}$x),
∴CD=$\frac{2}{x}-\frac{1}{2}x$,PB=2-x,
∴S=$\frac{1}{2}$CD•PB=$\frac{1}{2}$($\frac{2}{x}-\frac{1}{2}x$)(2-x)=$\frac{1}{4}{x}^{2}$-$\frac{1}{2}x$+$\frac{2}{x}$-1(0<x≤2);
②分三种情况:
i)如图3,当AB为对角线时,此时CQ与AB互相垂直平分,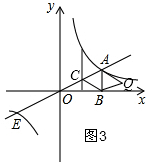
根据中点坐标公式得:C(1,$\frac{1}{2}$),Q(3,$\frac{1}{2}$);
ii)如图4,当AC为对角线时,此时过B作AC的垂线与AC交于点F,
∵∠AFB=∠ABO=90°,∠BAF=∠BAO,
∴△ABF∽△AOB,
∴$\frac{AF}{AB}=\frac{AB}{AO}$,
∴$\frac{AF}{1}=\frac{1}{\sqrt{5}}$,
∴AF=$\frac{\sqrt{5}}{5}$,AC=2AF=$\frac{2\sqrt{5}}{5}$,
∵C(x,$\frac{1}{2}$x),A(2,1),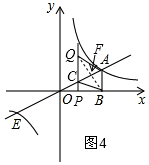
由两点之间的距离得:AC=$\frac{2\sqrt{5}}{5}$=$\sqrt{(x-2)^{2}+(\frac{1}{2}x-1)^{2}}$,
25x2-100x+84=0
(5x-6)(5x-14)=0
x1=$\frac{6}{5}$,x2=$\frac{14}{5}$>2(舍去),
∴OP=$\frac{6}{5}$,PC=$\frac{3}{5}$,PQ=PC+CQ=$\frac{3}{5}$+1=$\frac{8}{5}$,
则C($\frac{6}{5}$,$\frac{3}{5}$),Q($\frac{6}{5}$,$\frac{8}{5}$);
iii)如图5,当BC为对角线时,则AC=AB=1,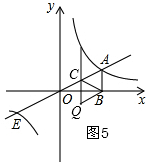
∵C(x,$\frac{1}{2}$x),A(2,1),
由两点之间的距离得:AC=1=$\sqrt{(x-2)^{2}+(\frac{1}{2}x-1)^{2}}$,
x1=2-$\frac{2\sqrt{5}}{5}$,x2=2+$\frac{2\sqrt{5}}{5}$,
∴C1$(2-\frac{2\sqrt{5}}{5},1-\frac{\sqrt{5}}{5})$,此时对应的Q(2-$\frac{2\sqrt{5}}{5}$,-$\frac{\sqrt{5}}{5}$);
C2$(2+\frac{2\sqrt{5}}{5},1+\frac{\sqrt{5}}{5})$,此时对应的Q(2+$\frac{2\sqrt{5}}{5}$,$\frac{\sqrt{5}}{5}$);
综上所述,点Q的坐标为:(3,$\frac{1}{2}$)或($\frac{6}{5}$,$\frac{8}{5}$)或(2-$\frac{2\sqrt{5}}{5}$,-$\frac{\sqrt{5}}{5}$)或(2+$\frac{2\sqrt{5}}{5}$,$\frac{\sqrt{5}}{5}$).
点评 本题是一次函数和反比例函数的综合题,考查了利用待定系数法求一次函数和反比例函数的解析式、交点问题与不等式解集的关系、两点的距离、菱形的性质和判定,采用分类讨论的思想,第二问利用数形结合直接找出不等式的解集.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “明天降雨的概率是75%”表示明天有75%的时间都在降雨 | |
| B. | “抛一枚硬币正面朝上的概率为$\frac{1}{2}$”表示每抛2次就有1次正面朝上 | |
| C. | “抛一枚均匀的正方体骰子,朝上的点数是2的概率为$\frac{1}{6}$”表示随着抛掷次数的增加,“抛出朝上的点数是2”这一事件发生的频率稳定在$\frac{1}{6}$左右 | |
| D. | “彩票中奖的概率为1%”表示买100张彩票肯定会中奖 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
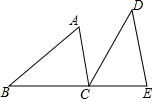 如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,BC=DE.
如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,BC=DE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
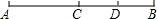 已知:如图,点C是线段AB的中点,点D是线段BC的中点,AB=20cm,那么线段AD等于( )
已知:如图,点C是线段AB的中点,点D是线段BC的中点,AB=20cm,那么线段AD等于( )| A. | 15cm | B. | 16cm | C. | 10cm | D. | 5cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com