练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

     2a4＋a3b2－5a2b3－1是_______次________项式．


    五、四； 

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    阅读理解并解答问题

       如果a、b、c为正整数，且满足a2+b2=c2，那么a、b、c叫做一组勾股数．

    (1) 例如3、4、5是一组勾股数，请写出一组不同于3、4、5的勾股数；

    (2) 如果m表示大于1的整数，且a=2m，b=m2—1，c=m2+1，请说明a、b、c为勾股数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    为庆祝“六一”儿童节，某幼儿园举行用火柴棒摆“金鱼”比赛．如图所示：

     


    按照上面的规律，摆个“金鱼”需用火柴棒的根数为（    ）

       A．           B．           C．          D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    小明在课外研究中，设计如下题目：直线y=kx+b过点A(6，0),B(0，3)，直线y=kx+b与曲线y=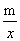(x>0)交于点C(4,n).

    （1）求出直线和曲线的解析式。（图1）

    图2
     

    图1
     

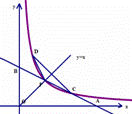
    （2）小明发现曲线y=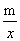(x>0)关于直线y=x对称，他把曲线y=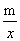(x>0)与直线y=x的交点 P叫做曲线的顶点。（图2）新课  标第  一 网

    ① 直接写出P点的坐标。

    ② 若点D从P点出发向上运动，运动到PD=PC时停止，求此时∆PCD的面积S.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在市委、市政府的领导下，全市人民齐心协力，将攀枝花成功地创建为“全国文明城市”，为此小红特制了一个正方体玩具，其展开图如图所示，原正方体中与“文”字所在的面，相对的面标的字应是（　 　）

    　   A．全   B．明   

    C．城                    D．国

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，AB∥CD，∠CDE=119°，GF交∠DEB的平分线EF于点F，∠AGF=130°，则∠F=________________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     如图1，E是直线AB，CD内部一点，AB∥CD，连接EA，ED．

    （1）探究猜想：①若∠A =25°，∠D =35°，则∠AED等于__________度.

    ②若∠A =35°，∠D =45°，则∠AED等于__________度.

    ③猜想图1中∠AED，∠EAB，∠EDC的关系并证明你的结论．

    （2）拓展应用：如图2，射线FE与矩形ABCD的边AB交于点E，与边CD交于点F，①②③④分别是被射线FE隔开的4个区域（不含边界，其中区域③、④位于直线AB上方，P是位于以上四个区域上的点，猜想：∠PEB，∠PFC，∠EPF的关系（直接写出结论，不要求证明）．

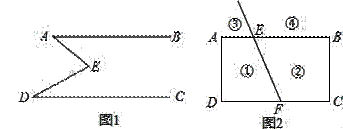
    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图所示，在8×8的网格中，我们把△ABC

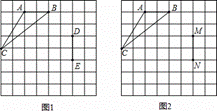    在图1中作轴对称变换，在图2中作旋转变换，

    已知网格中的线段ED、线段MN分别是边AB

    经两种不同变换后所得的像，请在两图中分别

    画出△ABC经各自变换后的像，并标出对称轴

    和旋转中心（要求：用无刻度的直尺，不写作法，

    但要保留作图痕迹）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    实数、在数轴上的位置如下图所示，则化简的结果为             （    　 ）

    A、  　 B、  　C、    D、

    查看答案和解析>>

    同步练习册答案