练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    （1）如图①，若BC=6，AC=4，∠C=60°，求△ABC的面积S△ABC ；

    （2）如图②，若BC=a，AC=b，∠C=α，求△ABC的面积S△ABC ；

    （3）如图③，四边形ABCD，若AC=m，BD=n，对角线AC、BD交于O点，它们所成的锐角为β．求四边形ABCD的面积S四边形ABCD ．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2014-2015学年山东省九年级中考适应性测试四数学试卷（解析版） 题型：填空题

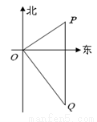
    小明在某风景区的观景台O处观测到东北方向的P处有一艘货船, 该船正向南匀速航 行30分钟后再观察时,该船已航行到O的南偏东30,且与O相距6km的Q处．如图所示．货船的航行速度是____________km/h．（结果用根号表示．）

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年山东省武城县九年级学业水平第一次模拟考试数学试卷（解析版） 题型：解答题

    如图，抛物线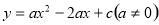交x轴于A.B两点，A点坐标为（3,0），与y轴交于C（0,4），以OC.OA为边作矩形OADC交抛物线于点G．

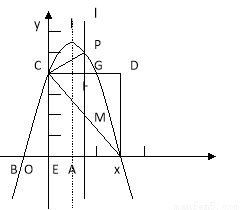
    （1）求抛物线的解析式；

    （2）平行于抛物线对称轴的直线l在边OA（不包括O、A两点）上平行移动，分别交x轴于点E，交CD于点F，交AC于点M，交抛物线于点P，若点M的横坐标为m，请用含m的代数式表示PM的长，并求PM长的最大值。

    （3）在（2）的条件下，连接PC,则在CD上方的抛物线部分是否存在这样的点P，使得以P、C.F为顶点的三角形和△AEM相似？若存在，求出此时m的值，并直接判断△PCM的形状；若不存在，请说明理由。

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年山东省武城县九年级学业水平第一次模拟考试数学试卷（解析版） 题型：选择题

    如图，一水库大坝的横断面为梯形ABCD，坝顶BC宽6米，坝高20米，斜坡AB的坡度i=1︰2.5，斜坡CD的坡角为30度，则坝底AD的长度为（ ）。

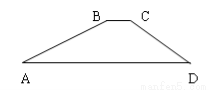
    A.56米 B.66米 C.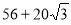（）米 D.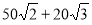（）米

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年山东省九年级中考第三次模拟数学试卷（解析版） 题型：解答题

    【课本节选】

    反比例函数y= （k为常数,k≠0）的图象是双曲线.当k＞0时，双曲线两个分支分别在三象限,在每一个象限内,y随x的增大而减小（简称增减性）；反比例函数的图象关于原点对称（简称对称性）．这些我们熟悉的性质，可以通过说理得到吗？

    【尝试说理】

    我们首先对反比例函数y=（k＞0）的增减性来进行说理．如图，当x＞0时．

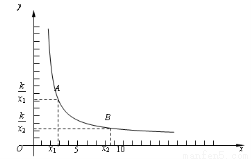
    在函数图象上任意取两点A、B，设A（x1，），B（x2，），

    且0＜x1＜ x2．

    下面只需要比较和的大小．

    —= ．

    ∵0＜x1＜ x2，∴x1－x2＜0，x1 x2＞0，且 k＞0．

    ∴＜0．即＜ ．

    这说明：x1＜ x2时，＞．也就是：自变量值增大了，对应的函数值反而变小了．

    即：当x＞0时，y随x的增大而减小．

    同理，当x＜0时，y随x的增大而减小．

    （1）试说明：反比例函数y= （k＞0）的图象关于原点对称．

    【运用推广】

    （2）分别写出二次函数y=ax2 （a＞0，a为常数）的对称性和增减性，并进行说理．

    对称性： ；

    增减性： ．

    说理：

    （3）对于二次函数y=ax2＋bx＋c （a＞0，a，b，c为常数），请你从增减性的角度，简要解释为何当x=— 时函数取得最小值．

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年山东省九年级中考第三次模拟数学试卷（解析版） 题型：计算题

    计算：

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年山东省九年级中考第三次模拟数学试卷（解析版） 题型：填空题

    （2×103）2×（3×10－3） = ．（结果用科学计数法表示）

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年山东省九年级学业水平5月模拟考数学试卷（解析版） 题型：填空题

    （本小题满分7分）

    学校为了解全校l 600名学生到校上学的方式，在全校随机抽取了若干名学生进行问卷调查．问卷给出五种上学方式供学生选择，每人只能选一项，且不能不选．将调查得到的结果绘制成如图所示的频数分布直方图和扇形统计图（均不完整）．（直接填写答案）

    （1）在这次调查中，一共要抽取学生__________名；

    （2）在这次调查中，抽取的学生中步行有__________名；

    （3）估计全校所有乘坐公交车上学的学生__________人．

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年山东省九年级下学期学业水平模拟考试数学试卷（解析版） 题型：解答题

    在Rt△ABC中，AB=BC，∠B=90°，将一块等腰直角三角板的直角顶点O放在斜边AC上，将三角板绕点O旋转．

    （1）当点O为AC中点时，

    ①如图1，三角板的两直角边分别交AB，BC于E、F两点，连接EF，猜想线段AE、CF与EF之间存在的等量关系（无需证明）；

    ②如图2，三角板的两直角边分别交AB，BC延长线于E、F两点，连接EF，判断①中的猜想是否成立？若成立，请证明；若不成立，请说明理由；

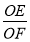    （2）当点O不是AC中点时，如图3，三角板的两直角边分别交AB，BC于E、F两点，若，求的值．

    查看答案和解析>>

    同步练习册答案