
����Ŀ���ڳ�����ABCD�У�AB��8cm��BC��4cm������P�ӵ�A��������·��A��B��C�������˶����ٶ�Ϊ2cm/�룬�˶���ʱ��Ϊt��.
��1���ú�t�Ĵ���ʽ��ʾ��P�˶���·��Ϊ cm����t��4.5ʱ����P�ڱ� �ϣ�
��2������P���߶�AB���˶�ʱ��д����ADP�����S��cm2����t���룩֮��Ĺ�ϵʽ������tΪ��ֵʱ��S��8��
��3���ڵ�P�˶��Ĺ����У���ADP����״Ҳ��֮�ı䣬�жϲ�ֱ��д��tΪ��ֵʱ����ADP�ǵ��������Σ�
���𰸡���1��2t��BC����2��![]() ����
����![]() ʱ��S=8����3����
ʱ��S=8����3����![]() ��
��![]() ʱ��ADP�ǵ���������.
ʱ��ADP�ǵ���������.
��������
��1������·��=�ٶ�![]() ʱ�䣬���ɵõ��𰸣�
ʱ�䣬���ɵõ��𰸣�
��2����AD=BC=4���������ε������ʽ�����ɵõ�S��t�Ĺ�ϵʽ��Ȼ���ٰ�S=8���룬���t��ֵ���ɣ�
��3���ɡ�ADP�ǵ��������Σ��ɷ�Ϊ����������ۣ��ٵ���P��AB��ʱ��AD=AP=4���ڵ���P��BC��ʱ����AP=DP�����㼴�ɵõ���.
��1����ͼ��
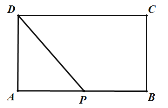
�߶���P�ӵ�A��������·��A��B��C�������˶����ٶ�Ϊ2cm/�룬�˶���ʱ��Ϊt�룬���ú�t�Ĵ���ʽ��ʾ��P�˶���·��Ϊ��![]() cm.
cm.
��t��4.5ʱ��·��Ϊ��![]() ��
��
��AB��8cm��8<9��
���Դ�ʱ��P�˶���BC�ϣ�
�ʴ�Ϊ��2t��BC��
��2�����ı���ABCD�dz����Σ�
��AD=BC=4��AP=2t��
��![]() ��
��
��S=4t����![]() ��
��
��S=8ʱ������ã�![]()
��![]() ��
��
��3���ߡ�ADP�ǵ��������Σ�
��AD=AP��AP=DP��
�ٵ���P��AB��ʱ����
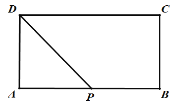
��AD=AP��
��2t=4����ã�![]() ��
��
�ڵ���P��BC��ʱ����
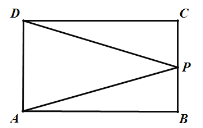
��AP=DP��
��ʱ��P��BC���е㣬
��![]() ��
��
��AB+BP=8+2=10��
���P�˶���ʱ��Ϊ��![]() s��
s��
�ۺ���������![]() ��
��![]() ʱ��ADP�ǵ��������Σ�
ʱ��ADP�ǵ��������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCֽƬ��DE�۵�����A�����ı���BCDE��ʱ�����A���1+��2֮����ʼ�ղ���Ĺ�ϵ�ǣ�������

A.��A=��1+��2B.2��A=��1+��2
C.3A=��1+��2D.3��A=2����1+��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �Ķ���ΪB��-1��3������
�Ķ���ΪB��-1��3������![]() ��Ľ���A�ڵ㣨-3��0���ͣ�-2��0��֮�䣬���½��ۣ���
��Ľ���A�ڵ㣨-3��0���ͣ�-2��0��֮�䣬���½��ۣ���![]() ����
����![]() ����
����![]() ����
����![]() �� ��
�� ��![]() ������ȷ���У�������
������ȷ���У�������
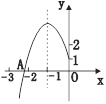
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ʵ�Ա�ﳵ���ʾֳ���������������2 km������A�壬������������3 km����B�壬Ȼ��������9 km����C�壬���ص��ʾ֣�
(1)���ʾ�Ϊԭ�㣬����Ϊ��������0.5 cm��ʾ1 km���������ᣬ���ڸ������ϱ�ʾ��A��B��C������ׯ��λ�ã�
(2)C����A���ж�Զ?
(3)�ʵ�Աһ�����˶���ǧ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������y=��x2+bx+c����A����1��0����B��4��0�����㣬��y���ཻ�ڵ�C������BC����PΪ��������һ���㣬����P��x��Ĵ���l����ֱ��BC�ڵ�G����x���ڵ�E��
��1���������ߵı���ʽ��
��2����Pλ��y���ұߵ����������˶�ʱ������C��CF��ֱ��l��FΪ���㣬����P�˶����δ�ʱ����P��C��FΪ���������������OBC���ƣ��������ʱ��P�����ꣻ

��3����ͼ2������P��λ��ֱ��BC�Ϸ������������˶�ʱ������PC��PB��������PBC�����S�ܷ�ȡ�����ֵ�����ܣ�������������S���������ʱ��P�����꣬�����ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ԭ�⣩��ֱ֪��AB��CD����PΪƽ����AB��CD֮���һ�㣮��ͼ1������ABP=50�㣬��CDP=60�㣬BEƽ����ABP��DEƽ����CDP������BED�Ķ�����
��̽������ͼ2������P��ֱ��AB���Ϸ�ʱ������ABP=������CDP=�£���ABP����CDP��ƽ���߽��ڵ�E1����ABE1����CDE1�Ľ�ƽ���߽��ڵ�E2����ABE2����CDE2�Ľ�ƽ���߽��ڵ�E3�����Դ����ƣ�����En�Ķ�����
����ʽ����ͼ3����ABP�Ľ�ƽ���ߵķ����ӳ��ߺ���CDP�IJ��ǵĽ�ƽ���߽��ڵ�E���Բ�����P����E��������ϵ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����У��ȫ���ܵ�ȫ���Ĺ㷺��ע��ij��ѧ�Բ���ѧ����У��ȫ֪ʶ���˽�̶ȣ����������������ķ�ʽ���������ռ�������Ϣ����ͳ�ƣ����������������в�������ͳ��ͼ�������ͳ��ͼ�����ṩ����Ϣ����������⣺
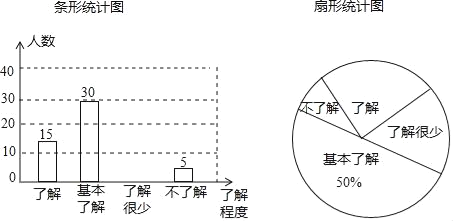
(1)�����ʾ������ѧ�������� ���ˣ�����ͳ��ͼ�С��˽⡱��������Ӧ���ε�Բ�Ľ�Ϊ�� ���ȣ�
(2)�벹ȫ����ͳ�ƣ�
(3)������ѧ����ѧ��1200�ˣ����Ƹ���ѧѧ����У��ȫ֪ʶ�ﵽ���˽⡱�͡������˽⡱�̶ȵ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������10�֣���һ������ȼ�������У��ס�����������ȼ��ʱʣ�ಿ�ֵĸ߶�![]() (����)��ȼ��ʱ��
(����)��ȼ��ʱ��![]() (Сʱ)֮��Ĺ�ϵ��ͼ��ʾ������������ȼ��ʱ
(Сʱ)֮��Ĺ�ϵ��ͼ��ʾ������������ȼ��ʱ![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��![]() .
.
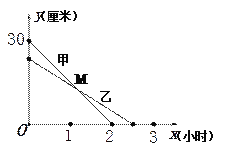
(1)������ȼ��ǰ�ĸ߶���_________����,������ȼ�յ�ʱ����________Сʱ.
(2)�������ȼ��ʱ![]() ��
��![]() ֮��ĺ�����ϵʽ.
֮��ĺ�����ϵʽ.
(3)���ͼ�н���![]() �����꣬��˵����
�����꣬��˵����![]() ��ʵ������.
��ʵ������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���߶�AB���߶�CD���ڵ�O,OEƽ�֡�AOC,��FΪ�߶�AB��һ��(�����A�͵�O�غ�)����F�� FG//OE,���߶�CD�ڵ�G,����AOD=110��,���AFG�Ķ���Ϊ_____��.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com