
分析 令(2x+y):1=(2y+z):2=(2z+u):3=(2u+x):4=k得2x+y=k①;2y+z=2k②;2z+u=3k③;2u+x=4k④;结合x+y+z+u=1可得k的值,代回①②③④方程得方程组,解方程组可得x、y、z、u的值,即可得代数式的值.
解答 解:设(2x+y):1=(2y+z):2=(2z+u):3=(2u+x):4=k,
∴2x+y=k①;2y+z=2k②;2z+u=3k③;2u+x=4k④;
①+②+③+④=3(x+y+z+u)=3=10k,
∴k=$\frac{3}{10}$,
联立①②③④可得:
$\left\{\begin{array}{l}{2x+y=\frac{3}{10}}\\{2y+z=\frac{3}{5}}\\{2z+u=\frac{9}{10}}\\{2u+x=\frac{6}{5}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=\frac{1}{25}}\\{y=\frac{11}{50}}\\{z=\frac{4}{25}}\\{u=\frac{29}{50}}\end{array}\right.$,
∴可得:7x+3y+3z+u=2.
故答案为:2.
点评 本题主要考查多元一次方程组和化归思想的应用能力,由比例式结合题意转化为解方程组是前提,化归中消元思想是解方程组的关键.


科目:初中数学 来源: 题型:解答题
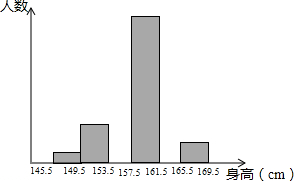 为了解某学校八年级学生的身体发育情况,学校对部分八年级女生的身高进行了一次测量,所得数据整理后绘制出统计图(如图)
为了解某学校八年级学生的身体发育情况,学校对部分八年级女生的身高进行了一次测量,所得数据整理后绘制出统计图(如图)| 组别 | 人数 | 百分比 |
| 145.5~149.5 | 1 | 2% |
| 149.5~153.5 | 4 | 8% |
| 153.5~157.5 | m | 40% |
| 157.5~161.5 | 15 | 30% |
| 161.5~165.5 | 8 | n |
| 165.5~169.5 | 2 | 4% |
| 合计 | 50 | 100% |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正△ABC的边长是2,点M是边AB上任意一点(可与A,B重合),作MD⊥BC于D,作DE⊥AC于E,作EN⊥AB于N,给出以下结论:①MN的最大值是$\frac{3}{2}$;②当M是AB的中点时,AN=$\frac{5}{8}$;③当M,N重合时,AN=$\frac{2}{3}$;④当△MBD≌△EAN时,AN=$\frac{1}{2}$,其中正确的结论有②③.
如图,正△ABC的边长是2,点M是边AB上任意一点(可与A,B重合),作MD⊥BC于D,作DE⊥AC于E,作EN⊥AB于N,给出以下结论:①MN的最大值是$\frac{3}{2}$;②当M是AB的中点时,AN=$\frac{5}{8}$;③当M,N重合时,AN=$\frac{2}{3}$;④当△MBD≌△EAN时,AN=$\frac{1}{2}$,其中正确的结论有②③.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com