Question

【题目】如图，△ABC是等边三角形，AN=BM，BN，MC相交于O，CH⊥BN于点H，求证：2OH=OC．

Answer 1

【答案】证明见解析.

【解析】

已知△ABC是等边三角形，根据等边三角形的性质可得AB=BC=AC，且三内角为60°，再由AN=BM，利用SAS得到△BAN≌△CBM，利用全等三角形的对应角相等及三角形外角的性质得到∠NOC=60°，在Rt△OHC中，利用30°角所对的直角边等于斜边的一半即可得2OH=OC．

∵△ABC为等边三角形，

∴AB=BC=AC，∠A=∠ABC=∠ACB=60°，

在△BAN和△CBM中，

，

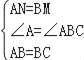∴△BAN≌△CBM（SAS），

∴∠ABN=∠BCM，

∵∠ABN+∠OBC=60°，

∴∠BCM+∠OBC=60°，

∵∠NOC为△OBC的外角，

∴∠NOC=∠BCM+∠OBC=60°，

在Rt△OHC，∠HCO=30°，

则2OH=OC．