
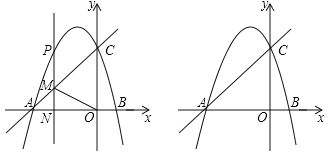
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于A、B两点,与y轴交于C.直线y=
x2+bx+c与x轴交于A、B两点,与y轴交于C.直线y=![]() x+3经过点A、C.
x+3经过点A、C.
(1)求抛物线的解析式;
(2)P是抛物线上一动点,过P作PM∥y轴交直线AC于点M,设点P的横坐标为t.
①若以点C、O、M、P为顶点的四边形是平行四边形,求t的值.
②当射线MP,AC,MO中一条射线平分另外两条射线的夹角时,直接写出t的值.
【答案】(1)![]() ;(2)①满足条件的t的值为2或﹣2+2
;(2)①满足条件的t的值为2或﹣2+2![]() 或﹣2﹣2
或﹣2﹣2![]() ;②综合以上可得t的值为
;②综合以上可得t的值为![]()
【解析】
(1)先根据直线解析式求出A、C两点的坐标,把点A和C点的坐标代入y=-![]() x2+bx+c得关于b和c的方程组,然后解方程组即可得到抛物线解析式;
x2+bx+c得关于b和c的方程组,然后解方程组即可得到抛物线解析式;
(2)当OC∥PM,且OC=PM时,以点C、O、M、P为顶点的四边形是平行四边形,可得关于t的方程,解方程即可;
(3)分三种情况考虑,当MP平分AC、MO的夹角,当AC平分MP、MO的夹角,当MO平分AC、MP的夹角,可由图形的性质得关于t的方程求解.
(1)在y=![]() x+3中,令x=0,y=3;令y=0,x=﹣4,得A(﹣4,0),C(0,3),
x+3中,令x=0,y=3;令y=0,x=﹣4,得A(﹣4,0),C(0,3),
代入抛物线y=-![]() x2+bx+c解析式得:
x2+bx+c解析式得: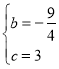 ,
,
∴抛物线的解析式![]() ;
;
(2)设P(t,![]() ),
),
∵四边形OCMP为平行四边形,
∴PM=OC=3,PM∥OC,
∴M点的坐标可表示为(t,![]() t+3),
t+3),
∴PM=![]() ,
,
∴|![]() =3,
=3,
当﹣![]() t2﹣3t=3,解得t=2,
t2﹣3t=3,解得t=2,
当﹣![]() t2﹣3t=﹣3,解得t1=﹣2+2
t2﹣3t=﹣3,解得t1=﹣2+2![]() ,t2=﹣2﹣2
,t2=﹣2﹣2![]() ,
,
综上所述,满足条件的t的值为2或﹣2+2![]() 或﹣2﹣2
或﹣2﹣2![]() ;
;
(3)如图1,

若当MP平分AC、MO的夹角,
则∠AMN=∠OMN,
∵PN⊥OA,
∴AN=ON,
∴t的值为﹣2;
如图2,

若AC平分MP、MO的夹角,过点C作CH⊥OA,CG⊥MP,
则CG=CH,
∵![]() ,
,
∴OM=OC=3,
∵点M在直线AC上,
∴M(t,![]() t+3),
t+3),
∴MN2+ON2=OM2,可得,![]() ,
,
解得t=﹣![]() ,
,
如图3,
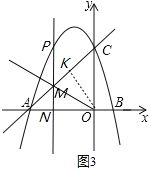
若MO平分AC、MP的夹角,则可得∠NMO=∠OMC,过点O作OK⊥AC,
∴OK=ON,
∵∠AKO=∠AOC=90°,∠OAK=OAC,
∴△AOK∽△ACO,
∴![]() ,
,
∴![]() ,
,
∴OK=![]() ,
,
∴t=﹣![]() ,
,
综合以上可得t的值为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
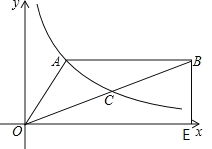
【题目】如图,双曲线y=![]() (x>0)经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3),BE⊥x轴,垂足为E.
(x>0)经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3),BE⊥x轴,垂足为E.
(1)确定k的值;
(2)若点D(3,m)在双曲线上,求直线AD的解析式;
(3)计算△OAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
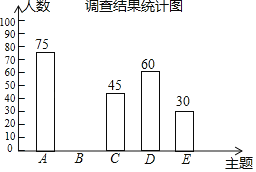
【题目】2019年3月19日,河南省教育厅发布《关于推进中小学生研学旅行的实施方案》,某中学为落实方案,给学生提供了以下五种主题式研学线路:A.“红色河南”,B.“厚重河南”C.“出彩河南”,D.“生态河南”,E.“老家河南”为了解学生最喜欢哪一种研学线路(每人只选取一种),随机抽取了部分学生进行调查,将调查结果绘制成如下不完整的统计表和统计图.根据以上信息解答下列问题:
调查结果统计表
主题 | 人数/人 | 百分比 |
A | 75 | n% |
B | m | 30% |
C | 45 | 15% |
D | 60 | |
E | 30 |
(1)本次接受调查的总人数为 人,统计表中m= ,n= .
(2)补全条形统计图.
(3)若把条形统计图改为扇形统计图,则“生态河南”主题线路所在扇形的圆心角度是 .
(4)若该实验中学共有学生3000人,请据此估计该校最喜欢“老家河南”主题线路的学生有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进A,B两种型号的手机,已知每部A型号手机的进价比每部B型号手机进价多500元,每部A型号手机的售价是2500元,每部B型号手机的售价是2100元.
(1)若商场用50000元共购进A型号手机10部,B型号手机20部,求A、B两种型号的手机每部进价各是多少元?
(2)为了满足市场需求,商场决定用不超过7.5万元采购A、B两种型号的手机共40部,且A型号手机的数量不少于B型号手机数量的2倍.
①该商场有哪几种进货方式?
②该商场选择哪种进货方式,获得的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
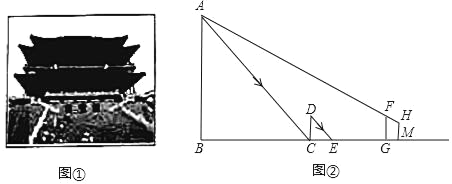
【题目】大唐芙蓉园是中国第一个全方位展示盛唐风貌的大型皇家园林式文化主题公园,全园标志性建筑一紫云楼为代表,展示了“形神升腾紫云景,天下臣服帝王心”的唐代帝王风范(如图①).小风和小花等同学想用一些测量工具和所学的几何知识测量“紫云楼”的高度,来检验自己掌握知识和运用知识的能力,他们经过研究需要两次测量:首先,在阳光下,小风在紫云楼影子的末端C点处竖立一根标杆CD,此时,小花测得标杆CD的影长CE=2米,CD=2米;然后,小风从C点沿BC方向走了5.4米,到达G处,在G处竖立标杆FG,接着沿BG后退到点M处时,恰好看见紫云楼顶端A,标杆顶端F在一条直线上,此时,小花测得CM=0.6米,小风的眼睛到地面的距离HM=1.5米,FG=2米.
如图②,已知AB⊥BM,CD⊥BM,FG⊥BM,HM⊥BM,请你根据题中提供的相关信息,求出紫云楼的高AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
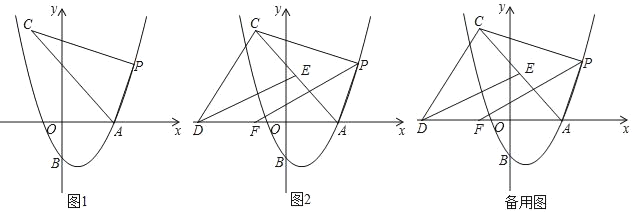
【题目】在平面直角坐标系中,点O为坐标原点,抛物线y=ax2﹣4ax﹣![]() 交x轴正半轴于点A(5,0),交y轴于点B.
交x轴正半轴于点A(5,0),交y轴于点B.
(1)求抛物线的解析式;
(2)如图1,点P为第一象限内抛物线上一点,连接AP,将射线AP绕点A逆时针旋转60°,与过点P且垂直于AP的直线交于点C,设点P横坐标为t,点C的横坐标为m,求m与t之间的函数关系式(不要求写出t的取值范围);
(3)如图2,在(2)的条件下,过点C作直线交x轴于点D,在x轴上取点F,连接FP,点E为AC的中点,连接ED,若F的横坐标为-![]() ,∠AFP=∠CDE,且∠FAP+∠ACD=180°,求m的值.
,∠AFP=∠CDE,且∠FAP+∠ACD=180°,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com