
【题目】在平面直角坐标系中,点O为坐标原点,抛物线y=ax2﹣4ax﹣![]() 交x轴正半轴于点A(5,0),交y轴于点B.
交x轴正半轴于点A(5,0),交y轴于点B.
(1)求抛物线的解析式;
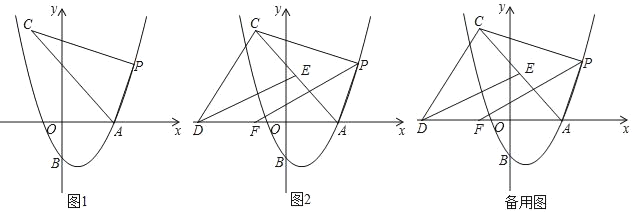
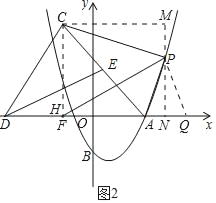
(2)如图1,点P为第一象限内抛物线上一点,连接AP,将射线AP绕点A逆时针旋转60°,与过点P且垂直于AP的直线交于点C,设点P横坐标为t,点C的横坐标为m,求m与t之间的函数关系式(不要求写出t的取值范围);
(3)如图2,在(2)的条件下,过点C作直线交x轴于点D,在x轴上取点F,连接FP,点E为AC的中点,连接ED,若F的横坐标为-![]() ,∠AFP=∠CDE,且∠FAP+∠ACD=180°,求m的值.
,∠AFP=∠CDE,且∠FAP+∠ACD=180°,求m的值.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() (2)m=
(2)m=![]() t2+
t2+![]() t+3(3)-
t+3(3)-![]()
【解析】
(1)把点A坐标代入即能求a的值.
(2)由AP⊥PC和旋转60°得∠PAC=60°得到特殊Rt△APC.利用已知点P、C的横坐标的条件,分别过点C、点P作坐标轴的垂线,构造三垂直模型下的相似,且相似比即为PC与AP的比![]() .用t、m表示相似三角形对应边的长度,利用相似比为
.用t、m表示相似三角形对应边的长度,利用相似比为![]() 列方程,即得到m与t的关系式.
列方程,即得到m与t的关系式.
(3)由特殊Rt△APC中∠ACP=30°与点E为AC的中点的条件得到CE=AE=AP;构造PQ=AP(Q在x轴上)得∠PAQ=∠PQA,再由∠FAP+∠ACD=180°和∠FAP邻补角为∠PAN得到∠ACD=∠PAN,即得到∠ACD=∠PAQ=∠PQA,因此构造的△QFP与△CDE全等,得到QF=CD.由四边形APCD内角和为360°可求得∠CDF=60°,作CH⊥x轴构造特殊直角三角形,利用CH=MN即可以t的式子表示CH,进而用t表示CD.又易由t的式子表示QF,列方程即求得t的值.再代回(2)的式子即求出m的值.
(1)∵抛物线y=ax2﹣4ax﹣![]() 过点A(5,0),
过点A(5,0),
∴25a﹣20a﹣![]() =0,
=0,
解得:a=![]() ,
,
∴抛物线的解析式为![]() ;
;
(2)过点P作MN⊥x轴于点N,过点C作CM⊥MN于点M,
∴∠M=∠ANP=90°,
∴∠MCP+∠CPM=90°.
∵CP⊥AP,
∴∠APC=90°,
∴∠CPM+∠APN=90°,
∴∠MCP=∠APN,
∴△MCP∽△NPA,
∴![]() ,
,
∵∠APC=90°,∠PAC=60°,
∴∠ACP=30°,tan∠PAC=![]() ,
,
∴![]() ,即
,即![]() .
.
∵xP=t,xC=m,
∴MC=t﹣m,PN=yP=![]() ,
,
∴t﹣m=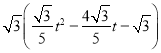 ,
,
整理得:m=![]() ,
,
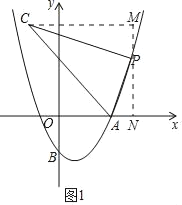
(3)过点C作CH⊥x轴于点H,在x轴上取点Q,连接PQ且使PQ=AQ,
∴∠CHD=90°,∠PAN=∠PQN,
∵∠ACP=30°,∠APC=90°,点E是AC中点,
∴AP=![]() AC=CE=AE,
AC=CE=AE,
∴CE=PQ,
∵∠FAP+∠ACD=180°,∠FAP+∠PAN=180°,
∴∠ACD=∠PAN,
∴∠ACD=∠PQN,
在△CDE与△QFP中
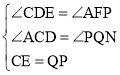 ,
,
∴△CDE≌△QFP(AAS),
∴CD=QF,
由(1)得,AN=t﹣5,PM=![]() ,PN=
,PN=![]() ,
,
∴CH=MN=PM+PN=![]() =
=![]() .
.
∵∠CDH=360°﹣∠CDP﹣∠APC﹣∠FAP=360°﹣(∠ACD+∠FAP)﹣∠ACP﹣∠APC=360°﹣180°﹣30°﹣90°=60°,
∴sin∠CDH=![]() ,
,
∴CD=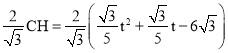 =
=![]() ,
,
∵F(﹣![]() ,0),
,0),
∴QF=AF+AQ=AF+2AN=5﹣(﹣![]() )+2(t﹣5)=2t﹣
)+2(t﹣5)=2t﹣![]() ,
,
∴![]() ,
,
解得:t1=﹣3,t2=7,
∵点P在第一象限,t>5,
∴t=7,
∴m=![]()
![]() .
.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:初中数学 来源: 题型:
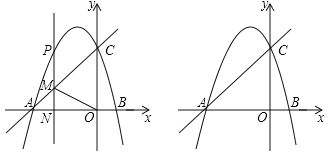
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于A、B两点,与y轴交于C.直线y=
x2+bx+c与x轴交于A、B两点,与y轴交于C.直线y=![]() x+3经过点A、C.
x+3经过点A、C.
(1)求抛物线的解析式;
(2)P是抛物线上一动点,过P作PM∥y轴交直线AC于点M,设点P的横坐标为t.
①若以点C、O、M、P为顶点的四边形是平行四边形,求t的值.
②当射线MP,AC,MO中一条射线平分另外两条射线的夹角时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
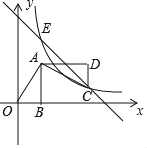
【题目】如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,点O的对应点C恰好落在双曲线y=![]() 的一个分支上,过C点的直线y=﹣x+b与双曲线的另一个交点为E,则△EOC的面积为_____.
的一个分支上,过C点的直线y=﹣x+b与双曲线的另一个交点为E,则△EOC的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级10个班的300名学生即将参加学校举行的研究旅行活动,学校提出以下4个活动主题:A.赤水丹霞地貌考察;B.平塘天文知识考察;C.山关红色文化考察;D.海龙电土司文化考察,为了解学生喜欢的活动主题,学生会开展了一次调查研究,请将下面的过程补全
(1)收集数据:学生会计划调查学生喜欢的活动主题情况,下面抽样调查的对象选择合理的是______.(填序号)
①选择七年级3班、4班、5班学生作为调查对象
②选择学校旅游摄影社团的学生作为调查对象
③选择各班学号为6的倍数的学生作为调查对象
(2)整理、描述数据:通过调査后,学生会同学绘制了如下两幅不完整的统计图,请把统计图补充完整
某校七年级学生喜欢的活动主题条形统计图某校七年级学生喜欢的活动主题扇形统计图
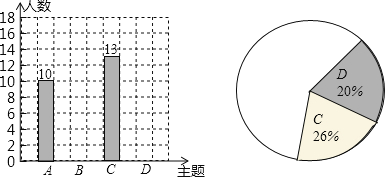
(3)分析数据、推断结论:请你根据上述调查结果向学校推荐本次活动的主题,你的推荐是______(填A-D的字母代号),估算全年级大约有多少名学生喜欢这个主题活动
(4)若在5名学生会干部(3男2女)中,随机选取2名同学担任活动的组长和副组长,求抽出的两名同学恰好是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系在代数和几何之间架起了一座桥梁,实现了几何方法与代数方法的结合,使数与形统一了起来,在平面直角坐标系中,已知点A(x1,y1)、B(x2,y2),则A、B两点之间的距离可以表示为AB=![]() ,例如A(2,1)、B(﹣1,2),则A、B两点之间的距离AB=
,例如A(2,1)、B(﹣1,2),则A、B两点之间的距离AB=![]() =
=![]() ;反之,代数式
;反之,代数式![]() 也可以看作平面直角坐标系中的点C(5,1)与点D(1,﹣2)之间的距离.
也可以看作平面直角坐标系中的点C(5,1)与点D(1,﹣2)之间的距离.
(1)已知点M(﹣7,6),N(1,0),则M、N两点间的距离为 ;
(2)求代数式![]() 的最小值;
的最小值;
(3)求代数式|![]() | 取最大值时,x的取值.
| 取最大值时,x的取值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状并说明理由.
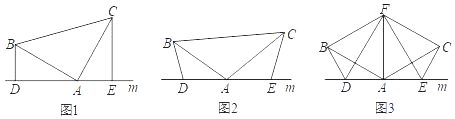
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是Rt△ABC斜边AB上的一点,⊙O经过点A与BC相切于点D,分别交AB,AC于E,F,OA=2cm,AC=3cm.
(1)求BE的长;
(2)求图中阴影部分的面积.
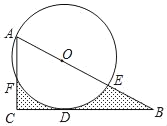
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+b与双曲线y=![]() (k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.
(k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.
(1)求直线和双曲线的解析式;
(2)点P在x轴上,且△BCP的面积等于2,求P点的坐标.
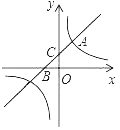
查看答案和解析>>
科目:初中数学 来源: 题型:
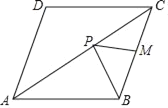
【题目】如图,已知菱形ABCD的面积为8![]() ,对角线AC长为4
,对角线AC长为4![]() ,M为BC的中点,若P为对角线AC上一动点,则PB与PM之和的最小值为( )
,M为BC的中点,若P为对角线AC上一动点,则PB与PM之和的最小值为( )
A. ![]() B. 2
B. 2![]() C. 2D. 4
C. 2D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com