
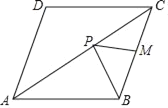
【题目】如图,已知菱形ABCD的面积为8![]() ,对角线AC长为4
,对角线AC长为4![]() ,M为BC的中点,若P为对角线AC上一动点,则PB与PM之和的最小值为( )
,M为BC的中点,若P为对角线AC上一动点,则PB与PM之和的最小值为( )
A. ![]() B. 2
B. 2![]() C. 2D. 4
C. 2D. 4
【答案】B
【解析】
作点B关于对角线AC的对称点,该对称点与D重合连接DM则PB与PM之和的最小值为DM的长;求出BD=4,∠ABC=120°,即可确定,△BCD是等边三角形,在Rt△CDM中,CM=2,CD=4,求得DM=2![]() .
.
作点B关于对角线AC的对称点,该对称点与D重合,
连接DM则PB与PM之和的最小值为DM的长;
∵菱形ABCD的面积为8![]() ,对角线AC长为4
,对角线AC长为4![]() ,
,
∴BD=4,
在Rt△ABO中,AO=2![]() ,BO=2,
,BO=2,
∴AB=4,
∴∠OAB=30°,
∴∠ABC=120°,
∴△BCD是等边三角形,
∵D是BC的中点,
∴DM⊥BC,
在Rt△CDM中,CM=2,CD=4,
∴DM=2![]() ,
,
故选B.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
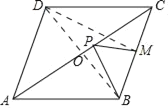
【题目】在平面直角坐标系中,点O为坐标原点,抛物线y=ax2﹣4ax﹣![]() 交x轴正半轴于点A(5,0),交y轴于点B.
交x轴正半轴于点A(5,0),交y轴于点B.
(1)求抛物线的解析式;
(2)如图1,点P为第一象限内抛物线上一点,连接AP,将射线AP绕点A逆时针旋转60°,与过点P且垂直于AP的直线交于点C,设点P横坐标为t,点C的横坐标为m,求m与t之间的函数关系式(不要求写出t的取值范围);
(3)如图2,在(2)的条件下,过点C作直线交x轴于点D,在x轴上取点F,连接FP,点E为AC的中点,连接ED,若F的横坐标为-![]() ,∠AFP=∠CDE,且∠FAP+∠ACD=180°,求m的值.
,∠AFP=∠CDE,且∠FAP+∠ACD=180°,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进甲、乙两种商品,甲种商品共用了2000元,乙种商品共用了2400元![]() 已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
![]() 求甲、乙两种商品的每件进价;
求甲、乙两种商品的每件进价;
![]() 该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变
该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变![]() 要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景点的门票价格如表
购票人数/人 | 1~40 | 41~80 | 80以上 |
每人门票价/元 | 10 | 8 | 6 |
某校九年级(1)、(2)两班计划去春游该景点,其中(1)班人数少于40人,(2)班人数多于40人且少于80人,如果两班都以班为单位单独购票,则一共支付838元:如果两班联合起来作为一个团体购票,则只需花费570元
(1)两个班各有多少名学生;
(2)团体购票与单独购票相比较,两个班各节约了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
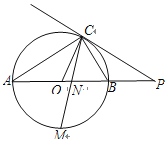
(1)求证:PC是⊙O的切线;
(2)求证:BC=![]() AB;
AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN![]() MC的值.
MC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】天水某公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车,计划购买A型和B型两行环保节能公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元,
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该条线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1220万元,且确保这10辆公交车在该线路的年均载客量总和不少于650万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的盒子,甲盒中装有编号为1,2,3三个球,乙盒中装有编号为4,5,6三个球,每个盒子中的球除编号外其它完全相同,将盒子中的球摇均后,从每个盒子中随机各取一个球.
(1)从甲盒中取出的球号数是3的概率是 ;
(2)请用列表法或画树状图法,求从两个盒子中取出的球号数都是偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
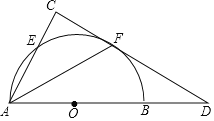
【题目】如图,已知AB是⊙O的直径,⊙O与Rt△ACD的两直角边分别交于点E、F,点F是弧BE的中点,∠C=90°,连接AF.
(1)求证:直线DF是⊙O的切线.
(2)若BD=1,OB=2,求tan∠AFC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某款篮球架的示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离(精确到0.01米)(参考数据:cos75°≈0.26,sin75°≈0.97,tan75°≈3.73,![]() ≈1.73)( )
≈1.73)( )
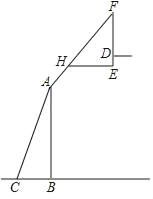
A. 3.04B. 3.05C. 3.06D. 4.40
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com