
【题目】某景点的门票价格如表
购票人数/人 | 1~40 | 41~80 | 80以上 |
每人门票价/元 | 10 | 8 | 6 |
某校九年级(1)、(2)两班计划去春游该景点,其中(1)班人数少于40人,(2)班人数多于40人且少于80人,如果两班都以班为单位单独购票,则一共支付838元:如果两班联合起来作为一个团体购票,则只需花费570元
(1)两个班各有多少名学生;
(2)团体购票与单独购票相比较,两个班各节约了多少钱?
【答案】(1)九年级(1)班有39人,九年级(2)班有56人;(2)九年级(1)班节省了156元,九年级(2)班节省了112元.
【解析】
(1)设九年级(1)班有x人,九年级(2)班有y人,根据总价=单价×数量结合“两班都以班为单位单独购票,则一共支付838元:如果两班联合起来作为一个团体购票,则只需花费570元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)根据节省的总钱数=每张票节省的钱数×人数,即可求出两个班各节约了多少钱.
(1)设九年级(1)班有x人,九年级(2)班有y人,
依题意,得:![]() ,
,
解得:![]() .
.
答:九年级(1)班有39人,九年级(2)班有56人.
(2)(10﹣6)×39=156(元),
(8﹣6)×56=112(元).
答:九年级(1)班节省了156元,九年级(2)班节省了112元.


科目:初中数学 来源: 题型:
【题目】某校七年级10个班的300名学生即将参加学校举行的研究旅行活动,学校提出以下4个活动主题:A.赤水丹霞地貌考察;B.平塘天文知识考察;C.山关红色文化考察;D.海龙电土司文化考察,为了解学生喜欢的活动主题,学生会开展了一次调查研究,请将下面的过程补全
(1)收集数据:学生会计划调查学生喜欢的活动主题情况,下面抽样调查的对象选择合理的是______.(填序号)
①选择七年级3班、4班、5班学生作为调查对象
②选择学校旅游摄影社团的学生作为调查对象
③选择各班学号为6的倍数的学生作为调查对象
(2)整理、描述数据:通过调査后,学生会同学绘制了如下两幅不完整的统计图,请把统计图补充完整
某校七年级学生喜欢的活动主题条形统计图某校七年级学生喜欢的活动主题扇形统计图
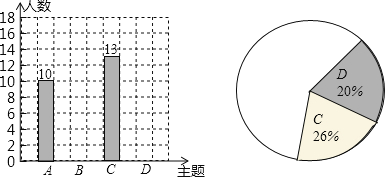
(3)分析数据、推断结论:请你根据上述调查结果向学校推荐本次活动的主题,你的推荐是______(填A-D的字母代号),估算全年级大约有多少名学生喜欢这个主题活动
(4)若在5名学生会干部(3男2女)中,随机选取2名同学担任活动的组长和副组长,求抽出的两名同学恰好是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
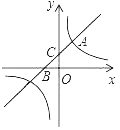
【题目】如图,直线y=x+b与双曲线y=![]() (k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.
(k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.
(1)求直线和双曲线的解析式;
(2)点P在x轴上,且△BCP的面积等于2,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
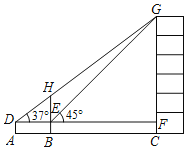
【题目】如图,某数学兴趣小组为测量一棵古树BH和教学楼CG的高,先在A处用高1.5米的测角仪测得古树顶端H的仰角∠HDE为37°,此时教学楼顶端G恰好在视线DH上,再向前走8米到达B处,又测得教学楼顶端G的仰角∠GEF为45°,点A、B、C三点在同一水平线上.
(1)求古树BH的高;
(2)计算教学楼CG的高度.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市水产养殖户进行小龙虾养殖.已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价p(元/千克)与时间第t(天)之间的函数关系为: ,日销售量y(千克)与时间第t(天)之间的函数关系如图所示:
,日销售量y(千克)与时间第t(天)之间的函数关系如图所示:
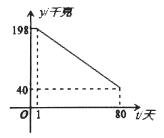
(1)求日销售量y与时间t的函数关系式?
(2)哪一天的日销售利润最大?最大利润是多少?
(3)该养殖户有多少天日销售利润不低于2400元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,线段AC的垂直平分线交AC于D点,交BC于E点,过点A作BC的平行线交直线ED于F点,连接AE,CF.
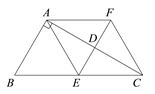
(1)求证:四边形AECF是菱形;
(2)若AB=10,∠ACB=30°,求菱形AECF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD的面积为8![]() ,对角线AC长为4
,对角线AC长为4![]() ,M为BC的中点,若P为对角线AC上一动点,则PB与PM之和的最小值为( )
,M为BC的中点,若P为对角线AC上一动点,则PB与PM之和的最小值为( )
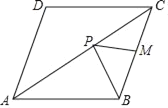
A. ![]() B. 2
B. 2![]() C. 2D. 4
C. 2D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC是等边三角形,点D是平面内一点,连接CD,将线段CD绕C顺时针旋转60°得到线段CE,连接BE,AD,并延长AD交BE于点P.
(1)当点D在图1所在的位置时
①求证:△ADC≌△BEC;
②求∠APB的度数;
③求证:PD+PE=PC;
(2)如图2,当△ABC边长为4,AD=2时,请直接写出线段CE的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点
经过点![]() 、
、![]() .
.![]() 是线段
是线段![]() 上一动点(点
上一动点(点![]() 不与
不与![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,交线段
,交线段![]() 于点
于点![]() .过点
.过点![]() 作
作![]() ,垂足为点
,垂足为点![]() .
.
[Failed to download image : http://192.168.0.10:8086/QBM/2019/5/18/2206393160556544/2207286529548288/STEM/a9696d0cbdac438aa94c80bfc838afd4.png]
(1)求该抛物线的解析式;
(2)试求线段![]() 的长
的长![]() 关于点
关于点![]() 的横坐标
的横坐标![]() 的函数解析式,并求出
的函数解析式,并求出![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com