
【题目】已知:如图,△ABC是等边三角形,点D是平面内一点,连接CD,将线段CD绕C顺时针旋转60°得到线段CE,连接BE,AD,并延长AD交BE于点P.
(1)当点D在图1所在的位置时
①求证:△ADC≌△BEC;
②求∠APB的度数;
③求证:PD+PE=PC;
(2)如图2,当△ABC边长为4,AD=2时,请直接写出线段CE的最大值.

【答案】(1)①见解析;②∠APB=60°;③见解析;(2)当∠ADC=90°时,CE取最大值为2![]() .
.
【解析】
(1)①根据旋转的性质和等边三角形的性质以及全等三角形的判定证明即可;
②根据全等三角形的判定和性质以及三角形内角和解答即可;
③根据等边三角形的性质以及全等三角形的判定和性质解答即可;
(2)当∠ADC=90°时,CE取最大值,进而利用直角三角形的性质解答即可.
(1)①∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=∠ACB=∠ABC=60°,
∵将线段CD绕C顺时针旋转60°得到线段CE,
∴CE=CD,∠DCE=60°,
∴△DCE是等边三角形,
∴∠DCE=60°,
∵∠ACD+∠DCB=60°,∠BCE+∠DCB=60°,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(SAS);
②∵△ACD≌△BCE,
∴∠EBC=∠DAC,
∵∠DAC+∠BAD=∠BAC=60°,
∴∠PBC+∠BAD=60°,
∴∠APB=180°﹣∠ABC+∠PBC+∠BAP=180°﹣60°﹣60°=60°;
③∵△ACD≌△BCE,
∴∠CBE=∠CAD,
∵∠CAD+∠BAD=60°,∠BAD+∠DBC=60°,
∴∠BAD+∠ABD=∠BDP=60°,
∵∠APB=60°,
∴△BDP是等边三角形,
∴DP=BP,
∴PD+PE=BE,
∵△ADC≌△BEC,
∴AD=BE,
∵在△ABD与△CBP中
 ,
,
∴△ABD≌△CBP(SAS),
∴AD=PC,
∴PD+PE=PC;
(2)当∠ADC=90°时,CE取最大值,
∵AB=AC=4,AD=2,
∴CD=![]() ,
,
∴CE=2![]() ,
,
即当∠ADC=90°时,CE取最大值为2![]() .
.


 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PA,PB,AB,已知∠PBA=∠C.

(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景点的门票价格如表
购票人数/人 | 1~40 | 41~80 | 80以上 |
每人门票价/元 | 10 | 8 | 6 |
某校九年级(1)、(2)两班计划去春游该景点,其中(1)班人数少于40人,(2)班人数多于40人且少于80人,如果两班都以班为单位单独购票,则一共支付838元:如果两班联合起来作为一个团体购票,则只需花费570元
(1)两个班各有多少名学生;
(2)团体购票与单独购票相比较,两个班各节约了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】天水某公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车,计划购买A型和B型两行环保节能公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元,
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该条线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1220万元,且确保这10辆公交车在该线路的年均载客量总和不少于650万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的盒子,甲盒中装有编号为1,2,3三个球,乙盒中装有编号为4,5,6三个球,每个盒子中的球除编号外其它完全相同,将盒子中的球摇均后,从每个盒子中随机各取一个球.
(1)从甲盒中取出的球号数是3的概率是 ;
(2)请用列表法或画树状图法,求从两个盒子中取出的球号数都是偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
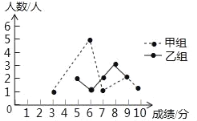
【题目】某校举行了一次古诗词朗读竞赛,满分为10分,学生得分均为整数,成绩达到6分及6分以上为合格.达到9分或10分为优秀.这次竞赛中,甲、乙两组学生成绩统计分析表和成绩分布的折线统计图如图所示.
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优率率 |
甲组 | 6.8 | a | 3.76 | 90% | 30% |
乙组 | b | 7.5 | 1.96 | 80% | 20% |
(1)求出成绩统计分析表中a的值.
(2)小英说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察成绩统计分析表判断,小英是甲、乙哪个组的学生.
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.试写出两条支持乙组同学观点的理由.
(4)从这次参加学校古诗词朗诵竞赛的甲、乙两组成绩优秀的学生中,随机抽取两名学生参加全市古诗词朗诵竞赛,恰好是乙组学生的概率是多少?(画树状图或列表求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
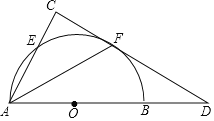
【题目】如图,已知AB是⊙O的直径,⊙O与Rt△ACD的两直角边分别交于点E、F,点F是弧BE的中点,∠C=90°,连接AF.
(1)求证:直线DF是⊙O的切线.
(2)若BD=1,OB=2,求tan∠AFC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
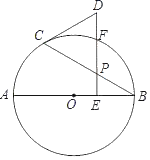
【题目】如图,已知AB是⊙O的直径,点P是弦BC上一动点(不与端点重合),过点P作PE⊥AB于点E,延长EP交![]() 于点F,交过点C的切线于点D.
于点F,交过点C的切线于点D.
(1)求证:△DCP是等腰三角形;
(2)若OA=6,∠CBA=30°.
①当OE=EB时,求DC的长;
②当![]() 的长为多少时,以点B,O,C,F为顶点的四边形是菱形?
的长为多少时,以点B,O,C,F为顶点的四边形是菱形?
查看答案和解析>>
科目:初中数学 来源: 题型:
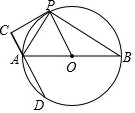
【题目】如图,已知AB是⊙O的直径,PC切⊙O于点P,过A作直线AC⊥PC交⊙O于另一点D,连接PA、PB.
(1)求证:AP平分∠CAB;
(2)若P是直径AB上方半圆弧上一动点,⊙O的半径为2,则
①当弦AP的长是_____时,以A,O,P,C为顶点的四边形是正方形;
②当![]() 的长度是______时,以A,D,O,P为顶点的四边形是菱形.
的长度是______时,以A,D,O,P为顶点的四边形是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com