
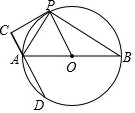
【题目】如图,已知AB是⊙O的直径,PC切⊙O于点P,过A作直线AC⊥PC交⊙O于另一点D,连接PA、PB.
(1)求证:AP平分∠CAB;
(2)若P是直径AB上方半圆弧上一动点,⊙O的半径为2,则
①当弦AP的长是_____时,以A,O,P,C为顶点的四边形是正方形;
②当![]() 的长度是______时,以A,D,O,P为顶点的四边形是菱形.
的长度是______时,以A,D,O,P为顶点的四边形是菱形.
【答案】(1)证明见解析;(2)①2![]() ;②
;②![]() π或
π或![]() π.
π.
【解析】
(1)利用切线的性质得OP⊥PC,再证明AC∥OP得到∠1=∠3,加上∠2=∠3,所以∠1=∠2;
(2)①当∠AOP=90°,根据正方形的判定方法得到四边形AOPC为正方形,从而得到AP=2![]() ;
;
②根据菱形的判定方法,当AD=AP=OP=OD时,四边形ADOP为菱形,所以△AOP和△AOD为等边三角形,然后根据弧长公式计算![]() 的长度.当AD=DP=PO=OA时,四边形ADPO为菱形,△AOD和△DOP为等边三角形,则∠AOP=120°,根据弧长公式计算
的长度.当AD=DP=PO=OA时,四边形ADPO为菱形,△AOD和△DOP为等边三角形,则∠AOP=120°,根据弧长公式计算![]() 的长度.
的长度.
(1)∵PC切⊙O于点P,
∴OP⊥PC,
∵AC⊥PC,
∴AC∥OP,
∴∠1=∠3,
∵OP=OA,
∴∠2=∠3,
∴∠1=∠2,
∴AP平分∠CAB;
(2)①当∠AOP=90°,四边形AOPC为矩形,而OA=OP,此时矩形AOPC为正方形,
AP=![]() OP=2
OP=2![]() ;
;
②当AD=AP=OP=OD时,四边形ADOP为菱形,△AOP和△AOD为等边三角形,则∠AOP=60°,![]() 的长度=
的长度=![]() =
=![]() π.
π.
当AD=DP=PO=OA时,四边形ADPO为菱形,△AOD和△DOP为等边三角形,则∠AOP=120°,![]() 的长度=
的长度=![]() .
.
故答案为2![]() ;
;![]() π或
π或![]() π.
π.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
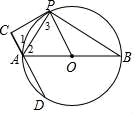
【题目】已知:如图,△ABC是等边三角形,点D是平面内一点,连接CD,将线段CD绕C顺时针旋转60°得到线段CE,连接BE,AD,并延长AD交BE于点P.
(1)当点D在图1所在的位置时
①求证:△ADC≌△BEC;
②求∠APB的度数;
③求证:PD+PE=PC;
(2)如图2,当△ABC边长为4,AD=2时,请直接写出线段CE的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点
经过点![]() 、
、![]() .
.![]() 是线段
是线段![]() 上一动点(点
上一动点(点![]() 不与
不与![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,交线段
,交线段![]() 于点
于点![]() .过点
.过点![]() 作
作![]() ,垂足为点
,垂足为点![]() .
.
[Failed to download image : http://192.168.0.10:8086/QBM/2019/5/18/2206393160556544/2207286529548288/STEM/a9696d0cbdac438aa94c80bfc838afd4.png]
(1)求该抛物线的解析式;
(2)试求线段![]() 的长
的长![]() 关于点
关于点![]() 的横坐标
的横坐标![]() 的函数解析式,并求出
的函数解析式,并求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
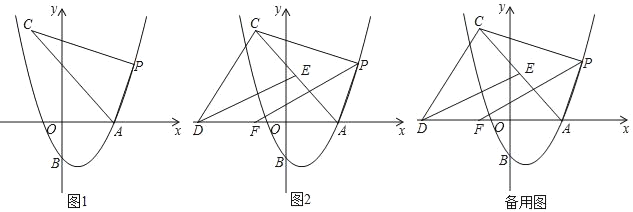
【题目】在平面直角坐标系中,点O为坐标原点,抛物线y=ax2﹣4ax﹣![]() 交x轴正半轴于点A(5,0),交y轴于点B.
交x轴正半轴于点A(5,0),交y轴于点B.
(1)求抛物线的解析式;
(2)如图1,点P为第一象限内抛物线上一点,连接AP,将射线AP绕点A逆时针旋转60°,与过点P且垂直于AP的直线交于点C,设点P横坐标为t,点C的横坐标为m,求m与t之间的函数关系式(不要求写出t的取值范围);
(3)如图2,在(2)的条件下,过点C作直线交x轴于点D,在x轴上取点F,连接FP,点E为AC的中点,连接ED,若F的横坐标为-![]() ,∠AFP=∠CDE,且∠FAP+∠ACD=180°,求m的值.
,∠AFP=∠CDE,且∠FAP+∠ACD=180°,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
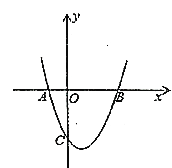
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点.
两点.
(1)求该抛物线的解析式;
(2)抛物线的对称轴上是否存在一点![]() ,使
,使![]() 的周长最小?若存在,请求出点
的周长最小?若存在,请求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
(3)设抛物线上有一个动点![]() ,当点
,当点![]() 在该抛物线上滑动到什么位置时,满足
在该抛物线上滑动到什么位置时,满足![]() ,并求出此时点
,并求出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
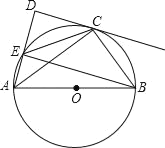
【题目】如图,AB是⊙O的直径,CD切⊙O于点C,AD交⊙O于点E,AC平分∠BAD,连接BE.
(1)求证:CD⊥ED;
(2)若CD=4,AE=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(x+y)2-2x(x+y); (2)(a+1)(a-1)-(a-1)2;
(3)先化简,再求值:
(x+2y)(x-2y)-(2x3y-4x2y2)÷2xy,其中x=-3,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级某班同学为了了解2012年某居委会家庭月均用水情况,随机调查了该居委会部分家庭,并将调查数据进行如下调整:
月均用水量x(t) | 频数(户) | 频率 |
0<x≤5 | 6 | 0.12 |
5<x≤10 | a | 0.24 |
10<x≤15 | 16 | 0.32 |
15<x≤20 | 10 | 0.20 |
20<x≤25 | 4 | 0.08 |
25<x≤30 | 2 | 0.04 |
请解答以下问题:
(1)频数分布表中a= ,把频数分布直方图补充完整;
(2)求该居委会用水量不超过15t的家庭占被调查家庭总数的百分比;
(3)若该居委会有1000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户?

查看答案和解析>>
科目:初中数学 来源: 题型:
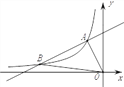
【题目】如图,一次函数y=k1x+b的图象与反比例函数y=![]() (x<0)的图象相交于点A(-1,2)、点B(-4,n).
(x<0)的图象相交于点A(-1,2)、点B(-4,n).
(1)求此一次函数和反比例函数的表达式;
(2)求△AOB的面积;
(3)在x轴上存在一点P,使△PAB的周长最小,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com