
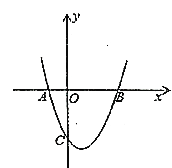
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点.
两点.
(1)求该抛物线的解析式;
(2)抛物线的对称轴上是否存在一点![]() ,使
,使![]() 的周长最小?若存在,请求出点
的周长最小?若存在,请求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
(3)设抛物线上有一个动点![]() ,当点
,当点![]() 在该抛物线上滑动到什么位置时,满足
在该抛物线上滑动到什么位置时,满足![]() ,并求出此时点
,并求出此时点![]() 的坐标.
的坐标.
【答案】(1)y=x2﹣2x﹣3;(2)存在;M(1,﹣2);(3)(1+2![]() ,4)或(1﹣2
,4)或(1﹣2![]() ,4)或(1,﹣4).
,4)或(1,﹣4).
【解析】
(1)由于抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点,那么可以得到方程x2+bx+c=0的两根为x=-1或x=3,然后利用根与系数即可确定b、c的值;
(2)点B是点A关于抛物线对称轴的对称点,在抛物线的对称轴上有一点M,要使MA+MC的值最小,则点M就是BC与抛物线对称轴的交点,利用待定系数法求出直线BC的解析式,把抛物线对称轴x=1代入即可得到点M的坐标;
(3)根据S△PAB=8,求得P的纵坐标,把纵坐标代入抛物线的解析式即可求得P点的坐标.
(1)∵抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,
∴方程x2+bx+c=0的两根为x=﹣1或x=3,
∴﹣1+3=﹣b,
﹣1×3=c,
∴b=﹣2,c=﹣3,
∴二次函数解析式是y=x2﹣2x﹣3.
(2)∵点A、B关于对称轴对称,
∴点M为BC与对称轴的交点时,MA+MC的值最小,
设直线BC的解析式为y=kx+t(k≠0),
则![]() ,解得:
,解得:![]() ,
,
∴直线AC的解析式为y=x﹣3,
∵抛物线的对称轴为直线x=1,
∴当x=1时,y=﹣2,
∴抛物线对称轴上存在点M(1,﹣2)符合题意;
(3)设P的纵坐标为|yP|,
∵S△PAB=8,
∴![]() AB|yP|=8,
AB|yP|=8,
∵AB=3+1=4,
∴|yP|=4,
∴yP=±4,
把yP=4代入解析式得,4=x2﹣2x﹣3,
解得,x=1±2![]() ,
,
把yP=﹣4代入解析式得,﹣4=x2﹣2x﹣3,
解得,x=1,
∴点P在该抛物线上滑动到(1+2![]() ,4)或(1﹣2
,4)或(1﹣2![]() ,4)或(1,﹣4)时,满足S△PAB=8.
,4)或(1,﹣4)时,满足S△PAB=8.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的盒子,甲盒中装有编号为1,2,3三个球,乙盒中装有编号为4,5,6三个球,每个盒子中的球除编号外其它完全相同,将盒子中的球摇均后,从每个盒子中随机各取一个球.
(1)从甲盒中取出的球号数是3的概率是 ;
(2)请用列表法或画树状图法,求从两个盒子中取出的球号数都是偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
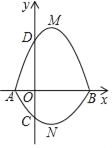
【题目】如图,抛物线C1:y=mx2﹣2mx﹣3m(m<0)与x轴交于A、B两点,与y轴交于点D,顶点为M,另一条抛物线C2与x轴也交于A、B两点,且与y轴的交点是C(0,![]() ),顶点是N.
),顶点是N.
(1)求A,B两点的坐标.
(2)求抛物线C2的函数表达式.
(3)是否存在m,使得△OBD与△OBC相似?若存在,请求出m的值;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某款篮球架的示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离(精确到0.01米)(参考数据:cos75°≈0.26,sin75°≈0.97,tan75°≈3.73,![]() ≈1.73)( )
≈1.73)( )
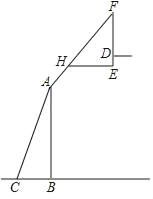
A. 3.04B. 3.05C. 3.06D. 4.40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:给定关于x的函数y,对于该函数图象上任意两点(x1,y1),(x2,y2),当x1=﹣x2时,都有y1=y2,称该函数为偶函数,根据以上定义,可以判断下面所给的函数中,是偶函数的有_____(填上所有正确答案的序号)
①y=2x;②y=﹣x+1;③y=x2;④y=﹣![]() ;⑤y=x2+3;⑥y=x2+2x+1.
;⑤y=x2+3;⑥y=x2+2x+1.
查看答案和解析>>
科目:初中数学 来源: 题型:
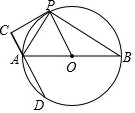
【题目】如图,已知AB是⊙O的直径,PC切⊙O于点P,过A作直线AC⊥PC交⊙O于另一点D,连接PA、PB.
(1)求证:AP平分∠CAB;
(2)若P是直径AB上方半圆弧上一动点,⊙O的半径为2,则
①当弦AP的长是_____时,以A,O,P,C为顶点的四边形是正方形;
②当![]() 的长度是______时,以A,D,O,P为顶点的四边形是菱形.
的长度是______时,以A,D,O,P为顶点的四边形是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CD是∠ACB的平分线,交AB于点D,过点D分别作AC、BC的平行线DE、DF,则下列结论错误的是( )
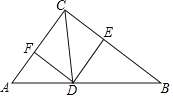
A. ![]() B.
B. ![]()
C. ![]() D. 四边形DECF是正方形
D. 四边形DECF是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数y=ax2+bx+c的图象过点(﹣1,0)和(m,0),请思考下列判断:①abc<0;②4a+c<2b;③![]() =1﹣
=1﹣![]() ;④am2+(2a+b)m+a+b+c<0;⑤|am+a|=
;④am2+(2a+b)m+a+b+c<0;⑤|am+a|=![]() 正确的是( )
正确的是( )
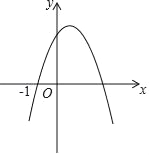
A. ①③⑤ B. ①②③④⑤ C. ①③④ D. ①②③⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com