
【题目】在平面直角坐标系中,点O为坐标原点,抛物线y=ax2﹣4ax﹣![]() 交x轴正半轴于点A(5,0),交y轴于点B.
交x轴正半轴于点A(5,0),交y轴于点B.
(1)求抛物线的解析式;
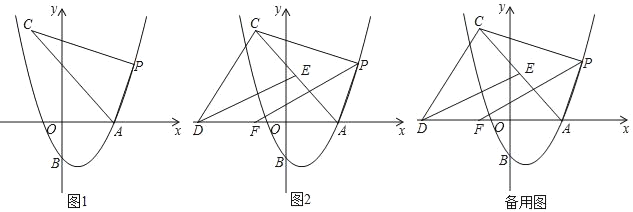
(2)如图1,点P为第一象限内抛物线上一点,连接AP,将射线AP绕点A逆时针旋转60°,与过点P且垂直于AP的直线交于点C,设点P横坐标为t,点C的横坐标为m,求m与t之间的函数关系式(不要求写出t的取值范围);
(3)如图2,在(2)的条件下,过点C作直线交x轴于点D,在x轴上取点F,连接FP,点E为AC的中点,连接ED,若F的横坐标为-![]() ,∠AFP=∠CDE,且∠FAP+∠ACD=180°,求m的值.
,∠AFP=∠CDE,且∠FAP+∠ACD=180°,求m的值.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() (2)m=
(2)m=![]() t2+
t2+![]() t+3(3)-
t+3(3)-![]()
【解析】
(1)把点A坐标代入即能求a的值.
(2)由AP⊥PC和旋转60°得∠PAC=60°得到特殊Rt△APC.利用已知点P、C的横坐标的条件,分别过点C、点P作坐标轴的垂线,构造三垂直模型下的相似,且相似比即为PC与AP的比![]() .用t、m表示相似三角形对应边的长度,利用相似比为
.用t、m表示相似三角形对应边的长度,利用相似比为![]() 列方程,即得到m与t的关系式.
列方程,即得到m与t的关系式.
(3)由特殊Rt△APC中∠ACP=30°与点E为AC的中点的条件得到CE=AE=AP;构造PQ=AP(Q在x轴上)得∠PAQ=∠PQA,再由∠FAP+∠ACD=180°和∠FAP邻补角为∠PAN得到∠ACD=∠PAN,即得到∠ACD=∠PAQ=∠PQA,因此构造的△QFP与△CDE全等,得到QF=CD.由四边形APCD内角和为360°可求得∠CDF=60°,作CH⊥x轴构造特殊直角三角形,利用CH=MN即可以t的式子表示CH,进而用t表示CD.又易由t的式子表示QF,列方程即求得t的值.再代回(2)的式子即求出m的值.
(1)∵抛物线y=ax2﹣4ax﹣![]() 过点A(5,0),
过点A(5,0),
∴25a﹣20a﹣![]() =0,
=0,
解得:a=![]() ,
,
∴抛物线的解析式为![]() ;
;
(2)过点P作MN⊥x轴于点N,过点C作CM⊥MN于点M,
∴∠M=∠ANP=90°,
∴∠MCP+∠CPM=90°.
∵CP⊥AP,
∴∠APC=90°,
∴∠CPM+∠APN=90°,
∴∠MCP=∠APN,
∴△MCP∽△NPA,
∴![]() ,
,
∵∠APC=90°,∠PAC=60°,
∴∠ACP=30°,tan∠PAC=![]() ,
,
∴![]() ,即
,即![]() .
.
∵xP=t,xC=m,
∴MC=t﹣m,PN=yP=![]() ,
,
∴t﹣m=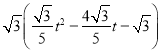 ,
,
整理得:m=![]() ,
,
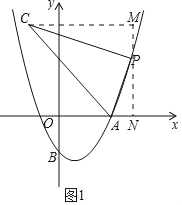
(3)过点C作CH⊥x轴于点H,在x轴上取点Q,连接PQ且使PQ=AQ,
∴∠CHD=90°,∠PAN=∠PQN,
∵∠ACP=30°,∠APC=90°,点E是AC中点,
∴AP=![]() AC=CE=AE,
AC=CE=AE,
∴CE=PQ,
∵∠FAP+∠ACD=180°,∠FAP+∠PAN=180°,
∴∠ACD=∠PAN,
∴∠ACD=∠PQN,
在△CDE与△QFP中
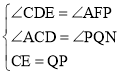 ,
,
∴△CDE≌△QFP(AAS),
∴CD=QF,
由(1)得,AN=t﹣5,PM=![]() ,PN=
,PN=![]() ,
,
∴CH=MN=PM+PN=![]() =
=![]() .
.
∵∠CDH=360°﹣∠CDP﹣∠APC﹣∠FAP=360°﹣(∠ACD+∠FAP)﹣∠ACP﹣∠APC=360°﹣180°﹣30°﹣90°=60°,
∴sin∠CDH=![]() ,
,
∴CD=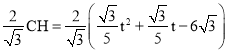 =
=![]() ,
,
∵F(﹣![]() ,0),
,0),
∴QF=AF+AQ=AF+2AN=5﹣(﹣![]() )+2(t﹣5)=2t﹣
)+2(t﹣5)=2t﹣![]() ,
,
∴![]() ,
,
解得:t1=﹣3,t2=7,
∵点P在第一象限,t>5,
∴t=7,
∴m=![]()
![]() .
.



科目:初中数学 来源: 题型:
【题目】天水某公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车,计划购买A型和B型两行环保节能公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元,
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该条线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1220万元,且确保这10辆公交车在该线路的年均载客量总和不少于650万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点P是弦BC上一动点(不与端点重合),过点P作PE⊥AB于点E,延长EP交![]() 于点F,交过点C的切线于点D.
于点F,交过点C的切线于点D.
(1)求证:△DCP是等腰三角形;
(2)若OA=6,∠CBA=30°.
①当OE=EB时,求DC的长;
②当![]() 的长为多少时,以点B,O,C,F为顶点的四边形是菱形?
的长为多少时,以点B,O,C,F为顶点的四边形是菱形?
查看答案和解析>>
科目:初中数学 来源: 题型:
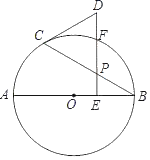
【题目】如图,平行四边形ABCD,F是对角线AC上的一点,过点D作DE∥AC,且DE=CF,连接AE、DE、EF.
(1)求证:△ADE≌△BCF;
(2)若∠BAF+∠AED=180°,求证:四边形ABFE为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
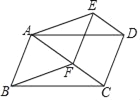
【题目】如图是某款篮球架的示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离(精确到0.01米)(参考数据:cos75°≈0.26,sin75°≈0.97,tan75°≈3.73,![]() ≈1.73)( )
≈1.73)( )
A. 3.04B. 3.05C. 3.06D. 4.40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,第一个正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4),延长CB交x轴于点A1,作第二个正方形A1B1C1C;延长C1B1交x轴于点A2,作第三个正方形A2B2C2C1…按这样的规律进行下去,第2018个正方形的面积为( )

A. 20×(![]() )2017 B. 20×(
)2017 B. 20×(![]() )2018 C. 20×(
)2018 C. 20×(![]() )4036 D. 20×(
)4036 D. 20×(![]() )4034
)4034
查看答案和解析>>
科目:初中数学 来源: 题型:
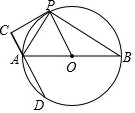
【题目】如图,已知AB是⊙O的直径,PC切⊙O于点P,过A作直线AC⊥PC交⊙O于另一点D,连接PA、PB.
(1)求证:AP平分∠CAB;
(2)若P是直径AB上方半圆弧上一动点,⊙O的半径为2,则
①当弦AP的长是_____时,以A,O,P,C为顶点的四边形是正方形;
②当![]() 的长度是______时,以A,D,O,P为顶点的四边形是菱形.
的长度是______时,以A,D,O,P为顶点的四边形是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
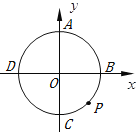
【题目】如图,半径为![]() 且坐标原点为圆心的圆交
且坐标原点为圆心的圆交![]() 轴、
轴、![]() 轴于点
轴于点![]() 、
、![]() 、
、![]() 、
、![]() ,过圆上的一动点
,过圆上的一动点![]() (不与
(不与![]() 重合)作
重合)作![]() ,且
,且![]() (
(![]() 在
在![]()
![]() 右侧)
右侧)
(1)连结![]() ,当
,当![]() 时,则点
时,则点![]() 的横坐标是______.
的横坐标是______.
(2)连结![]() ,设线段
,设线段![]() 的长为
的长为![]() ,则
,则![]() 的取值范围是____.
的取值范围是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
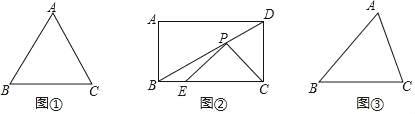
【题目】问题探究:
(1)如图①,已知等边△ABC,边长为4,则△ABC的外接圆的半径长为 .
(2)如图②,在矩形ABCD中,AB=4,对角线BD与边BC的夹角为30°,点E在为边BC上且BE=![]() BC,点P是对角线BD上的一个动点,连接PE,PC,求△PEC周长的最小值.
BC,点P是对角线BD上的一个动点,连接PE,PC,求△PEC周长的最小值.
问题解决:
(3)为了迎接新年的到来,西安城墙举办了迎新年大型灯光秀表演.其中一个镭射灯距城墙30米,镭射灯发出的两根彩色光线夹角为60°,如图③,若将两根光线(AB,AC)和光线与城墙的两交点的连接的线段(BC)看作一个三角形,记为△ABC,那么该三角形周长有没有最小值?若有,求出最小值,若没有,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com