练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，抛物线经过点、.是线段上一动点（点不与、重合），过点作轴的垂线交抛物线于点，交线段于点.过点作，垂足为点.

    [Failed to download image : http://192.168.0.10:8086/QBM/2019/5/18/2206393160556544/2207286529548288/STEM/a9696d0cbdac438aa94c80bfc838afd4.png]

    （1）求该抛物线的解析式；

    （2）试求线段的长关于点的横坐标的函数解析式，并求出的最大值.

    【答案】（1）；（2）=，当时，取最大值，.

    【解析】

    （1）把代入解析式即可求出抛物线的解析式；（2）利用得，求得，再求出直线BC的解析式为，得点坐标为，坐标为

    ∴= ，即可表示出DF的函数为- ，即可求出最值.

    （1）∵抛物线过点。

    ∴可得，解得

    ∴抛物线的解析式为

    （2）∵

    ∴，∴

    ∴，∴

    ∴

    ∵，∴

    ∴

    ∵直线经过点

    ∴，∴点坐标为

    ∵点坐标为

    ∴

    =

    ∴

    =

    =

    ∴当时，取最大值，

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知AB是⊙O的直径，弦CD⊥AB于H，过CD延长线上一点E作⊙O的切线交AB的延长线于F，切点为G，连接AG交CD于K．

    （1）如图1，求证：KE=GE；

    （2）如图2，连接CABG，若∠FGB=∠ACH，求证：CA∥FE；

    （3）如图3，在（2）的条件下，连接CG交AB于点N，若sinE=，AK=，求CN的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线分别交x轴、y轴于点A(2，0)、B(0，4)，点P是线段AB上一动点，过点P作PC⊥x轴于点C，交抛物线于点D．

    (1)若．

    ①求抛物线的解析式；

    ②当线段PD的长度最大时，求点P的坐标；

    (2)当点P的横坐标为1时，是否存在这样的抛物线，使得以B、P、D为顶点的三角形与△AOB相似？若存在，求出满足条件的抛物线的解析式；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

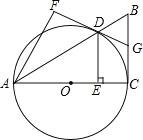
    【题目】如图，已知Rt△ABC中，∠ACB=90°，以AC为直径的圆O交斜边AB于D．过D作DE⊥AC于E，将△ADE沿直线AB翻折得到△ADF．

    （1）求证：DF是⊙O的切线；

    （2）若⊙O的半径为10，sin∠FAD=，延长FD交BC于G，求BG的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

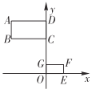
    【题目】如图,矩形的两边在坐标轴上,点为平面直角坐标系的原点,以轴上的某一点为位似中心,作位似图形,且点的坐标,则位似中心的坐标为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

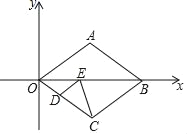
    【题目】如图，在平面直角坐标系中，菱形OABC的顶点A的坐标为（4，3），点D是边OC上的一点，点E在直线OB上，连接DE、CE，则DE+CE的最小值为（　　）

    A. 5B. +1C. 2D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，O为Rt△ABC斜边中点，AB=10，BC=6，M，N在AC边上，∠MON=∠B，若△OMN与△OBC相似，则CM=_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

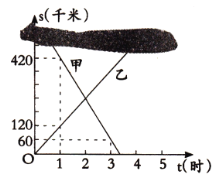
    【题目】甲、乙两列火车分别从，两城同时匀速驶出，甲车开往城，乙车开往城.由于墨迹遮盖，图中提供的只是两车距城的路程 （千米），（千米）与行驶时间（时）的函数图象的一部分.

    （1）乙车的速度为_______________千米时；

    （2）分别求出，与的函数解析式（不必写出的取值范围）；

    （3）求出两城之间的路程，及为何值时两车相遇；

    （4）当两车相距千米时，求的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

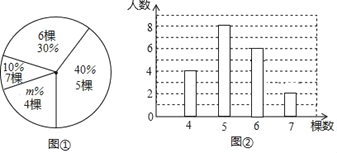
    【题目】某校260名学生参加植树活动，活动结束后学校随机调查了部分学生每人的植树棵数，并绘制成如下的统计图①和统计图②．请根据相关信息，解答下列问题：

    (Ⅰ)本次接受调查的学生人数为______，图①中m的值为_______；

    (Ⅱ)求本次调查获取的样本数据的众数和中位数；

    (Ⅲ)求本次调查获取的样本数据的平均数，并根据样本数据，估计这260名学生共植树多少棵．

    查看答案和解析>>

    同步练习册答案