
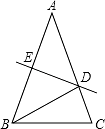
如图,△ABC 中,AB=AC=5,AB 的垂直平分线 DE 交 AB、AC 于 E、D.
(1)若△BCD 的周长为 8,求 BC 的长; 若 ∠A=40°,求∠DBC 的度数.
∠A=40°,求∠DBC 的度数.
【考点】线段垂直平分线的性质;等腰三角形的性质.
【分析】(1)根据线段垂直平 分线定理得出 AD=BD,根据 BC+CD+BD=8cm 求出 AC+BC=8cm,把 AC 的长代入求出即可;
分线定理得出 AD=BD,根据 BC+CD+BD=8cm 求出 AC+BC=8cm,把 AC 的长代入求出即可;
已知∠A=40°,AB=AC 可得∠ABC=∠ACB,再由线段垂直平分线的性质可求出∠ABC=∠A,易求
∠DBC.
【解答】解:(1)∵D 在 AB 垂直平分线上,
∴AD=BD,
∵△BCD 的周长为 8cm,
∴BC+CD+BD=8cm,
∴AD+DC+BC=8cm,
∴AC+BC=8cm,
∵AB=AC=5cm,
∴BC=8cm﹣5 cm=3cm;
cm=3cm;
∵∠A=40°,AB=AC,
∴∠ABC=∠ACB=70°,
又∵DE 垂直平分 AB,
∴DB=AD
∴∠ABD=∠A=40°,
∴∠DBC=∠ABC﹣∠ABD=70°﹣40°=30°.
【点评】本题考查了等腰三角形性质和线段垂直平分线定理,关键是求出 AC+BC 的值,注意:线 段垂直平分线上的点到线段的两端点的距离相等.


科目:初中数学 来源: 题型:
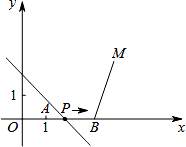
如图,A(1,0),B(3,0),M(4,3),动点 P 从点 A 出发,沿 x 轴以每秒 1 个单位的速度 向右移动,经过点 P 的直线 l:y=﹣x+b 也随之移动,设移动时间为 t 秒.
(1)当 t=1 时,求 l 的解析式;
若 l 与线段 BM 有公共点,确定 t 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
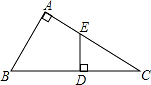
如图,D 为 Rt△ABC 中斜边 BC 上的一点,且 BD=AB,过 D 作 BC 的垂线,交 AC 于 E,若 AE=12cm,则 DE 的长为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
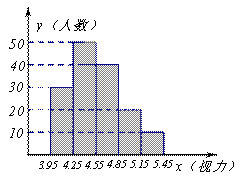
当今,青少年视力水平下降已引起了社会的关注,为了了解某校3000名学生的视力情况,从中抽取了一部分学生进行了一次抽样调查,利用所得数据绘制的条形图(长方形的高表示该组人数)如下:
请解答下列问题:
(1)本次抽样调查共抽测了多少名学生?
(2)参加抽测学生的视力的众数在什么范围内?
(3)若视力为4.9,5.0,5.1及以上为正常,试估计该校学生视力正常的人数约为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com